I have a generic 360 Camera, and when I convert its fisheye 235° output into equirectangular using FFMpeg, I don't get good results, the image appears squeezed at the bottom.
How could I determine the exact transformation needed to properly convert my images into equirectangular? FFMpeg has a "remap" filter, which uses 2 .pgm files for remapping... but how do I crate such files for my camera?
There is also lensfun and lenscorrection , but question is the same: how do I tune them for my camera?
I am using the generic filter v360 with these parameters:
ffmpeg -i input.jpg -vf v360=fisheye:e:ih_fov=235:iv_fov=235 -y output.jpg
These are 2 croppings on a detail of the equirectangular output:
Look at how much the car is squeezed!
This also cause 360 video stabilization to fail due to too much distortion.
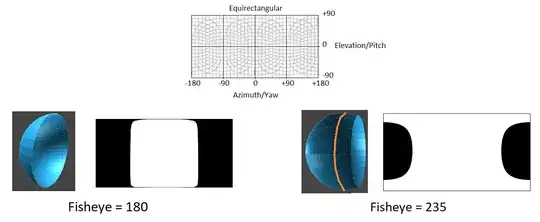
Some explanatory images:
Distortion of my camera highlighting by shooting a chessboard:
Probably I should instead get something like this, i.e. squares getting bigger and bigger as they come closer:
The target:
Additional images: