IF the filters in Bayer masks created three discrete color ranges in which any particular wavelength could only pass through a single filter, then the resolution would be 1/2 for the "green" filtered wavelengths and 1/4 for the "blue" and "red" filtered wavelengths.
IF the filters in Bayer masks created three discrete color ranges in which any particular wavelength could only pass through a single filter, then color reproduction that looks anything like what our eye/brain systems perceive would also be impossible.
This is because there is no such thing as "color" in wavelengths of light. Color is a perception constructed by an eye/brain system that detects certain wavelengths of light due to a chemical response in the retinas of those eyes. This perception of color is due to the brain comparing the differences in response to the same light by the three types of cones in human retinas. The response of the three types of cones in the human retina have a LOT of overlap, particularly in the 'M' (medium wavelengths) and 'L' (long wavelengths) cones.
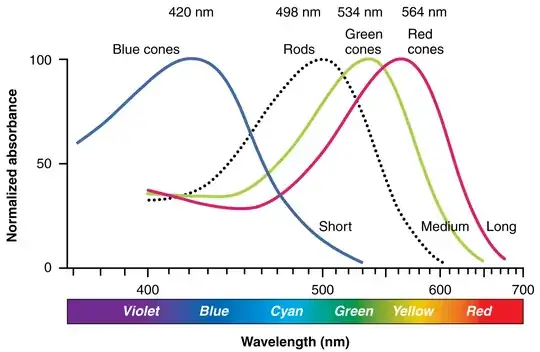
Please note that our "red" cones are most sensitive to light at wavelengths which we typically call "yellow" rather than red. It is only in our trichromatic color reproductions systems (printing presses and electronic screens that use three "primary" colors to, hopefully, produce a similar response from our eye/brain systems) that "red" is sometimes a primary color
If the filters in a Bayer mask did not also allow this overlapping of the response curves of each of the three filter colors, then our cameras could not interpolate color information from the results in the same way that our brains create color from the overlapping response of our retinal cones to various wavelengths of light.
Typical response curves of a modern Bayer masked digital sensor:
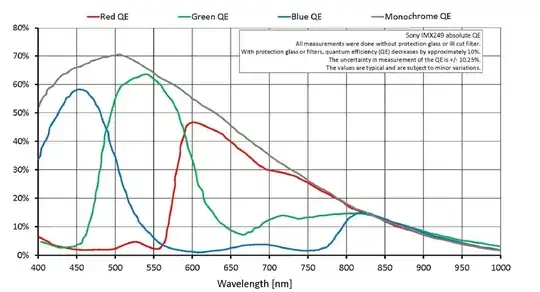
Because of the way that the human eye/brain systems works, the range of wavelengths to which our "green" cones are most sensitive affect our perception of fine details/local contrast much more than the ranges of wavelengths to which our "blue" and "red (yellow)" cones are sensitive. Our best demosaicing algorithms take this into account, and the colors interpolated for each photosite are weighted to imitate the way our eye/brain systems do it, rather than just doing a simple "nearest neighbors" interpolation method.
Keep in mind that since the peak colors of each of the Bayers mask's filters are not the same colors as the three primary colors in our RGB color reproductions systems, all three values for each of the three channels in RGB color must be interpolated, not just the "other missing two" colors.
Compare the peak sensitivities of the bayer filters compared to the colors used in our RGB TV/monitor screens (a few also include a yellow channel)
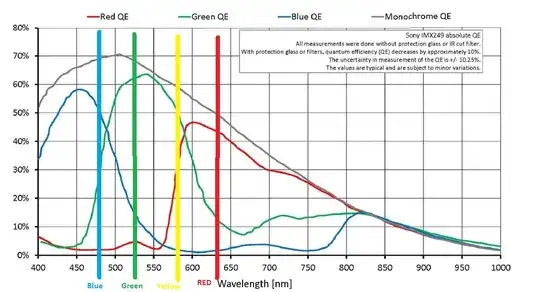
So even though our camera sensors only have half of their photosites (a/k/a pixel wells) filtered with green, the information that those "green" photosites record has a greater effect on our perception of fine details than the information recorded by the "blue" and "red (yellow)" photosites do. When all of this is combined, an optimally interpolated image from a Bayer masked sensor produces the same perceived resolution as if we take a monochrome sensor with 1/√2 as many pixels, shoot three images with three different color filters centered on our RGB primary colors completely covering all of the sensor's photosites, and combine those values to produce RGB values for each photosite.


