Lenses with very narrow angles of view require front elements that are roughly equivalent to the size of the entrance pupil. A typical telephoto prime lens will have a front element less than 10% larger than the entrance pupil at the lens' maximum aperture. This is because the light rays collected by the lens are almost perpendicular to the imaging plane and the entrance pupil will not be much larger than the diameter of the front element.
But with wider angles of view and their closer subject distances, the entrance pupil can be much larger than the front element:
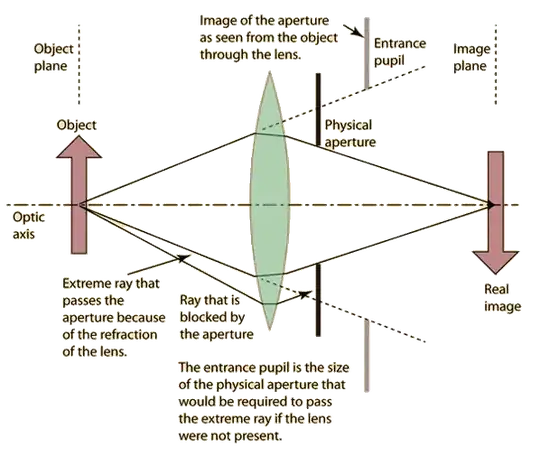
A simple single element lens:
A multiple element compound lens:
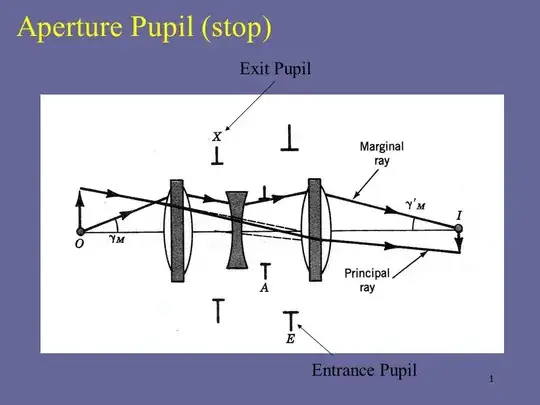
If the front element of a wider angle lens were only large enough for the entrance pupil to be fully visible from subjects centered on the lens' optical axis, the lens would severely vignette the light coming from the off axis portions of the frame. Thus wide angle lenses tend to have much larger front elements than the size of the entrance pupil so that a larger portion of the entrance pupil is visible from the more peripheral parts of the field of view.
When portions of the lens' field of view are obstructed from a full view of the entrance pupil, it can result in dark corners and oddly shaped out of focus highlights. Consider wide aperture lenses with even a normal field of view:

Such a lens is said to have "cat's eye" bokeh:

Even when there is no mechanical vignetting caused by the lens barrel, from wider angles the entrance pupil appears to be an oblong shape, rather than a circle.

Compare these examples, all intended for full frame cameras:
- Canon EF 300mm f/4 has 77mm filter threads. 300mm/4 is 75mm
- Canon EF 100mm f/2 has 58mm filter threads. 100mm/2 is 50mm
- Canon EF 85mm f/1.8 has 58mm filter threads. 85/1.8 is 47mm
- Canon EF 50mm f/1.4 has 58mm filter threads. 50mm/1.4 is 36mm
- Canon EF 35mm f/2 has 67mm filter threads. 35/2 is 17 mm
- Canon EF 24mm f/1.4 has 77mm filter threads. 24mm/1.4 is 17mm
Your 24-240mm f/3.5-6.3 lens having a near 72mm wide front element probably is more about reducing vignetting at 24mm and f/3.5 than it is about the needed entrance pupil for 240mm and f/6.3.




