11

Background

This question is about games that were created, developed, deployed and popularized1 by researchers because they wanted to learn more about some mathematical structure, and did so by collecting data and analyzing the strategies of other people2 playing the game. I wonder whether there are any examples in which researchers adopted such an approach.

SONNAT

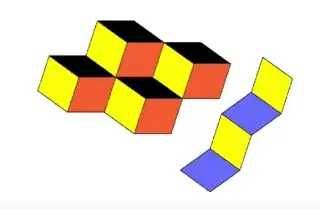
There is a game that in my eyes may be an appropriate candidate for such a line of action. It is called SONNAT, which stands for Same Orientation Neighbour Not Allowed, Tiling. It is a single player tiling game3 in which one's goal is to tile the plane with two rhombi. The first rhombus has inner angles with 72, 108, 72, and 108 degrees, respectively. It has a different colour for each of its 360/36 = 10 orientations. The second rhombus has inner angles with degrees 36, 144, 36, and 144 degrees. It always has the same colour, regardless of its orientation.

These two tiles are the same shapes that are employed to create the Penrose P3 aperiodic tiling. However, there is a catch: two rules are put in place that ensure the tiling differs from the original P3 tiling. The first one is that no two rhombi with the same colour (orientation) are allowed to be joined to one another along their sides. The second is that no "repeating patterns" may be formed with the tiles. Below are two examples of such repeating patterns. These repeating patterns are of length two. Repeating patterns of a higher length aren't allowed either.

                                                 enter image description here

By imposing these rules, players must strategically choose and place the tiles, so as to put as many tiles on the plane as possible. Below I show an example of an attempt to tile the plane in the SONNAT setting:

                          enter image description here

I think that, in this case, researchers could learn a great deal from peoples' strategies to play the game. They may not need to be professional mathematicians in order to come up with strategies that researchers did not devise themselves.

Now, SONNAT is not deployed in this manner. The code is open-source, but there is no mechanism through which the original inventor of the game can gain access to the data that shows how other people play the game, through which he can possibly gain knowledge4 on effective strategies to play it.

What this question is not about

I think it is relevant to point out there are a number of classes of games, and research written on them, that do not pertain to this question. These include:

  1. Games that have been popular for a long time, and were analyzed from a mathematical perspective later on. Examples of such games are chess, Go, and Hex. More examples can be found over here.
  2. Games developed for the purpose of educating younger students, but are not necessarily interesting or deep from a mathematical point of view. Examples of such games are described in this article, for instance.
  3. The research on the game is conducted in order to understand the underlying mathematics of that game, not human behaviour. So the study of humans5 in evolutionary game theory or studies of players avoiding a viral outbreak in an MMORPG do not encompass answers to this question.

Question

Are there any examples of games6 developed purposely for mathematics research, in which the researcher(s) analyze the data on the strategies that have been employed by the players?

Notes

1 It might even be the case that the inventor of the game allows some commercial party to popularize the game and host it in an online setting, in exchange for information on the data of people's (successful) strategies. In such a case, players would have to consent that their data may be used for research purposes.

2 It would, of course, be appropriate if the players that have come up with innovative strategies would be cited by the researchers who eventually write a paper on the subject, or be listed as co-authors.

3 Developed by someone with the pseudonym Pembesita. See his video here. I've asked an MO question on it before.

4 As Sam Hopkins pointed out, these are generally called Human-based computation games (HBCGs). A link to the relevant wiki page is provided here. It appears that no mathematical HBCG has been listed yet.

5 But if these humans actually devise techniques to play games better than the current state of the art in mathematics research, then it does count as an example, as suggested by R. van Dobben de Bruyn.

6 Note that we employ the term "game" in a broad, colloquial sense here. It is not necessarily tied up with the notion in game theory (though games arising from this theory are certainly not excluded). The SONNAT game, for example, may be more appropriately described as a puzzle, instead of a game.

Max Muller
  • 4,505
  • 3
    See https://en.wikipedia.org/wiki/Human-based_computation_game for something similar, but mostly in other scientific fields – Sam Hopkins Mar 03 '24 at 14:32
  • @SamHopkins Thank you for this pointer, I hadn't heard of the term before. Interesting that no mathematical games are described on the wiki page. – Max Muller Mar 03 '24 at 15:09
  • Does octal game qualify? – Max Alekseyev Mar 03 '24 at 20:07
  • 3
    Not sure if it's exactly what you're looking for, but the first results on optimal strategies for the iterated prisoner's dilemma were obtained by hosting tournaments were participants could submit algorithms. – R. van Dobben de Bruyn Mar 03 '24 at 20:24
  • Please use a larger typeface for your "Notes". Also, the first rhombus has infinitely many orientations, not just ten (though I think I know what you mean). – Gerry Myerson Mar 03 '24 at 21:18
  • @MaxAlekseyev I willl look into your and R. van Dobben de Bruyn's suggestions, and will try to judge to what extent they fit into this question. Either way: thank you for pointing them out to me – Max Muller Mar 03 '24 at 21:53
  • It looks as if the black rhombi form a third type of rhombus used in the tiling. – Daniel Asimov Mar 03 '24 at 22:26
  • If I properly understood your question, you are looking for games that were developed in the area called "Experimental Game Theory", and have been tested by researchers on humans. This is a rich area of research, where people study existing games (like the ultimatum game or the prisoner's dilemma), and sometimes invent new games to test some hypothesis. – Eilon Mar 04 '24 at 05:52
  • 2
    @Eilon I think that the ultimatum game, and many other games in experimental game theory, were devised in order to understand human behavior, rather than to study mathematical structure. So it doesn't seem to quite fit what Max Muller is asking for. – Timothy Chow Mar 04 '24 at 18:19
  • @Eilon Timothy Chow has worded my intent behind the question well – Max Muller Mar 04 '24 at 22:07
  • @DanielAsimov There are two types of tiles. The coloured rhombi have 10 different orientations, and each orientation has a different colour. The other tile is the slim rhombus, and is always black -- regardless of its orientation – Max Muller Mar 04 '24 at 22:09
  • @MaxAlekseyev I don't think it qualifies, because there was no study conducted by a researcher to find out whether the strategies of others could aid in discovering new mathematical structures or results in the game, right? Or am I missing something? – Max Muller Mar 05 '24 at 20:51
  • I once made a game still available here: http://tricky-animals.de/ where the aim of the game is to sort the animals in the given order by using only three buttons A,X,B. The gamer must also find out, what the buttons do by pressing them. It is based on the fact that the symmetric group of $n$ objects can be generated by three permutations (corresponding to the three buttons: https://puzzling.stackexchange.com/questions/43447/algorithm-for-solving-the-permutation-puzzle-tricky-animals). However I did not further continue this avenue for some reasons. It could be used in teaching finite groups. – mathoverflowUser Mar 06 '24 at 13:01
  • 1
    It could be used to gather data for specific puzzles to later be analysed how the puzzled were solved and the user interface is very spartanic for a game, is should be more playful, probably with some interactive help and visualization. But in the first step it was just a proof of concept, which still is online after 8 years. :-) – mathoverflowUser Mar 06 '24 at 13:05

0 Answers0