Does the formal power series solution to $f(f(x))= \sin( x) $ converge?

Question

I have spent some time using gp-pari. There is, of course, a formal power series solution to $ f(f(x)) = \sin x.$ It is displayed below, identified by the symbol $g$ because I am not entirely sure whether it is a function of anything.

On the other hand, should the coefficients continue to (by and large) decrease, this suggests a nonzero radius of convergence. If the radius of convergence is nonzero, then inside that, not only is a function defined and, you know, analytic, but the functional equation is satisfied. Indeed, all that is necessary is radius of convergence strictly larger than $\frac{\pi}{2}$ owing to certain symmetries. For instance, given my polynomial $g,$ it seems we have $g=1$ at about $x \approx 1.14.$ Then we seem to have a local maximum at $x =\frac{\pi}{2},$ and apparently there $g \approx 1.14,$ strictly larger than 1 which is an important point. So everything would fall into place with large enough nonzero radius of convergence.

\begin{align} g ={} & x - \frac{x^3 }{ 12} - \frac{x^5 }{ 160} - \frac{53 x^7 }{ 40320} - \frac{23 x^9 }{71680} - \frac{92713 x^{11}}{1277337600} \\[10pt] & - \frac{742031 x^{13} }{79705866240} + \frac{594673187 x^{15} }{167382319104000} + \frac{329366540401 x^{17} }{91055981592576000} + \\[10pt] & +\frac{104491760828591 x^{19} }{62282291409321984000} + \frac{1508486324285153 x^{21} }{4024394214140805120000} + \cdots \end{align}

Note that the polynomial $g$ is smaller than $x$ but larger that $\sin x,$ for, say, $0 < x \leq \frac{\pi}{2}.$

So, that is the question, does the formal power series beginning with $g$ converge anywhere other than $x = 0$?

EDIT: note that the terms after the initial $x$ itself have all turned out to be $$ \frac{a_{2 k + 3} x^{2 k + 3} }{2^k ( 2 k + 4)!} $$ where each $a_{2 k + 3}$ is an integer. This much seems provable, although I have not tried yet.

EDIT, Friday 12 November 2010. It now seems really unlikely that this particular problem gives an analytic answer. I suspect that the answer is $C^\infty$ and piecewise analytic, with failure of analyticity at only the points "parabolic" where the derivative has absolute value as large as 1, those points being $0,\pi, 2 \pi, \ldots.$ However, we need the anchor point at the fixpoint 0, otherwise how to begin? And I do think the power series will serve as an asymptotic expansion around 0.

Given the problem with the size of the derivative, now I am hoping for great things, and an obviously periodic and analytic solution, to the easier variant $f(f(x)) = g(x) = (1/2) \sin x.$ I would like both a nice power series and a nice answer by methods summing iterates $ g^{[k]}(x),$ which for the moment is an entirely mysterious method to me, but attractive for periodic target functions as periodicity would be automatic.

Answer 1

EDIT, September 2014: I wrote to Prof. Ecalle, it turns out (as I had hoped) that the fractional iterates constructed by the recipe below really do come out $C^\infty,$ including a growth bound, in terms of $n,$ on the $n$-th derivatives at $0.$ The key word phrase is Gevrey Class. Also, I recently put a better exposition and example of the technique at https://math.stackexchange.com/questions/911818/how-to-get-fx-if-we-know-ffx-x2x/912324#912324

EDIT Feb. 2016: given that there is new discussion of this, i am pasting in the mathematical portion of Prof. Ecalle's reply, which includes the references

Yes, indeed, any $f(x)$ real analytic at $0$ and of the form

$$f(x)=x+ ax^{p+1} +o(x^{p+1}) \text{ for } a \not= 0\tag{$*$} $$

admits natural fractional iterates $g=f^{o w}$ (right or left of zero) that are not just $C^\infty$ at $0$, but of Gevrey class $1/p$, i.e. with bounds of type

$$| g^{(n)}(0)/n! |< c_0 \cdot c_1^n \cdot (n/p)! \tag{$**$}$$

Here, $g$ may denote any iterate of rational or real order $w$. You may find details in my publication no 7 on my homepage http://www.math.u-psud.fr/~ecalle/publi.html or again in publication no 16 ("Six Lectures etc"; in English), pp 106-107 , Example 2 (with $\nu=1$).

Here, Gevrey smoothness at $0$ results from $g(x^{1/p})$ being the Laplace transform of an analytic function with (at worst) exponential growth at infinity.

The "Six Lectures" are in Schlomiuk editor, 1993, Bifurcations and periodic orbits of vector fields / edited by Dana Schlomiuk. The reference is currently number 19 on Ecalle's web page, it reads:

Six Lectures on Transseries, Analysable Functions and the Constructive Proof of Dulac's Conjecture . Bifurcations and Periodic Orbits of Vector Fields, D. Schlomiuk ed., p.75-184, 1993, Kluwer

ORIGINAL: The correct answer to this belongs to the peculiar world of complex dynamics. See John Milnor, Dynamics in One Complex Variable.

First, an example. Begin with $f(z) = \frac{z}{1 + z},$ which has derivative $1$ at $z=0$ but, along the positive real axis, is slightly less than $x$ when $x > 0.$ We want to find a Fatou coordinate, which Milnor (page 107) denotes $\alpha,$ that is infinite at $0$ and otherwise solves what is usually called the Abel functional equation, $$ \alpha(f(z)) = \alpha(z) + 1.$$ There is only one holomorphic Fatou coordinate up to an additive constant. We take $$ \alpha(z)= \frac{1}{ z}.$$ To get fractional iterates $f_s(z)$ of $f(z),$ with real $0 \leq s \leq 1,$ we take $$ f_s (z) = \alpha^{-1} \left( s + \alpha(z) \right) $$ and finally $$f_s(z) = \frac{z}{1 + s z}.$$ The desired semigroup homomorphism holds, $$ f_s(f_t(z)) = f_{s + t}(z), $$ with $f_0(z) = z$ and $f_1(z) = f(z).$

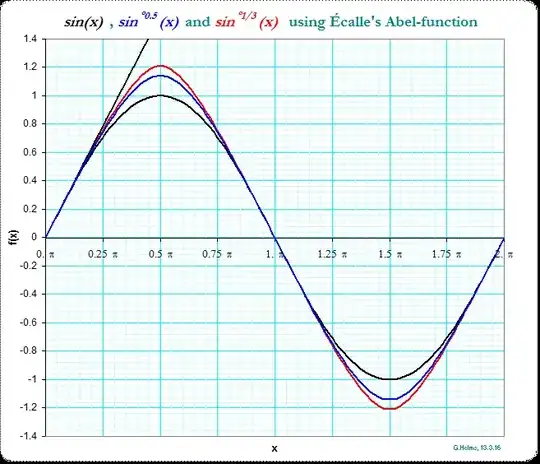
Alright, the case of $\sin z$ emphasizing the positive real axis is not terribly different, as long as we restrict to the interval $ 0 < x \leq \frac{\pi}{2}.$ For any such $x,$ define $x_0 = x, \; x_1 = \sin x, \; x_2 = \sin \sin x,$ and in general $ x_{n+1} = \sin x_n.$ This sequence approaches $0$, and in fact does so for any $z$ in a certain open set around the interval $ 0 < x \leq \frac{\pi}{2}$ that is called a petal.

Now, given a specific $x$ with $x_1 = \sin x$ and $ x_{n+1} = \sin x_n$ it is a result of Jean Ecalle at Orsay that we may take $$ \alpha(x) = \lim_{n \rightarrow \infty} \; \; \; \frac{3}{x_n^2} \; + \; \frac{6 \log x_n}{5} \; + \; \frac{79 x_n^2}{1050} \; + \; \frac{29 x_n^4}{2625} \; - \; n.$$

EDIT, August 2023: David Speyer has pointed out that the most direct expression of what Ecalle proved comes in $$ \alpha(x) = \lim_{n \rightarrow \infty} \; \; \; \frac{3}{x_n^2} \; + \; \frac{6 \log x_n}{5} \; - \; n.$$ I believe I included the $x_n^2, x_n^4$ terms because that was how I got the computer program (output below) to give small error ( the final column).

BACK to ORIGINAL

Note that $\alpha$ actually is defined on $ 0 < x < \pi$ with $\alpha(\pi - x) = \alpha(x),$ but the symmetry also means that the inverse function returns to the interval $ 0 < x \leq \frac{\pi}{2}.$

Before going on, the limit technique in the previous paragraph is given in pages 346-353 of Iterative Functional Equations by Marek Kuczma, Bogdan Choczewski, and Roman Ger. The solution is specifically Theorem 8.5.8 of subsection 8.5D, bottom of page 351 to top of page 353. Subsection 8.5A, pages 346-347, about Julia's equation, is part of the development.

As before, we define ( at least for $ 0 < x \leq \frac{\pi}{2}$) the parametrized interpolating functions, $$ f_s (x) = \alpha^{-1} \left( s + \alpha(x) \right) $$

In particular $$ f_{1/2} (x) = \alpha^{-1} \left( \frac{1}{2} + \alpha(x) \right) $$

I calculated all of this last night. First, by the kindness of Daniel Geisler, I have a pdf of the graph of this at:

http://zakuski.math.utsa.edu/~jagy/sine_half.pdf

Note that we use the evident symmetries $ f_{1/2} (-x) = - f_{1/2} (x)$ and $ f_{1/2} (\pi -x) = f_{1/2} (x)$

The result gives an interpolation of functions $f_s(x)$ ending at $ f_1(x)=\sin x$ but beginning at the continuous periodic sawtooth function, $x$ for $ -\frac{\pi}{2} \leq x \leq \frac{\pi}{2},$ then $\pi - x$ for $ \frac{\pi}{2} \leq x \leq \frac{3\pi}{2},$ continue with period $2 \pi.$ We do get $ f_s(f_t(z)) = f_{s + t}(z), $ plus the holomorphicity and symmetry of $\alpha$ show that $f_s(x)$ is analytic on the full open interval $ 0 < x < \pi.$

EDIT, TUTORIAL: Given some $z$ in the complex plane in the interior of the equilateral triangle with vertices at $0, \sqrt 3 + i, \sqrt 3 - i,$ take $z_0 = z, \; \; z_1 = \sin z, \; z_2 = \sin \sin z,$ in general $z_{n+1} = \sin z_n$ and $z_n = \sin^{[n]}(z).$ It does not take long to show that $z_n$ stays within the triangle, and that $z_n \rightarrow 0$ as $n \rightarrow \infty.$

Second, say $\alpha(z)$ is a true Fatou coordinate on the triangle, $\alpha(\sin z) = \alpha(z) + 1,$ although we do not know any specific value. Now, $\alpha(z_1) - 1 = \alpha(\sin z_0) - 1 = \alpha(z_0) + 1 - 1 = \alpha(z_0).$ Also $\alpha(z_2) - 2 = \alpha(\sin(z_1)) - 2 = \alpha(z_1) + 1 - 2 = \alpha(z_1) - 1 = \alpha(z_0).$ Induction, given $\alpha(z_n) - n = \alpha(z_0),$ we have $\alpha(z_{n+1}) - (n+1) = \alpha(\sin z_n) - n - 1 = \alpha(z_n) + 1 - n - 1 = \alpha(z_0).$

So, given $z_n = \sin^{[n]}(z),$ we have $\alpha(z_n) - n = \alpha(z).$

Third , let $L(z) = \frac{3}{z^2}+ \frac{6 \log z}{5} + \frac{79 z^2}{ 1050} + \frac{29 z^4}{2625}$. This is a sort of asymptotic expansion (at 0) for $\alpha(z),$ the error is $| L(z) - \alpha(z) | < c_6 |z|^6.$ It is unlikely that putting more terms on $L(z)$ leads to a convergent series, even in the triangle.

Fourth, given some $ z =z_0$ in the triangle. We know that $z_n \rightarrow 0$. So $| L(z_n) - \alpha(z_n) | < c_6 |z_n|^6.$ Or $| (L(z_n) - n ) - ( \alpha(z_n) - n) | < c_6 |z_n|^6 ,$ finally $$ | (L(z_n) - n ) - \alpha(z) | < c_6 |z_n|^6 .$$ Thus the limit being used is appropriate.

Fifth, there is a bootstrapping effect in use. We have no actual value for $\alpha(z),$ but we can write a formal power series for the solution of a Julia equation for $\lambda(z) = 1 / \alpha'(z),$ that is $\lambda(\sin z ) = \cos z \; \lambda(z).$ The formal power series for $\lambda(z)$ begins (KCG Theorem 8.5.1) with $- z^3 / 6,$ the first term in the power series of $\sin z$ after the initial $z.$ We write several more terms, $$\lambda(z) \asymp - \frac{z^3}{6} - \frac{z^5}{30} - \frac{41 z^7}{3780} - \frac{4 z^9}{945} \cdots.$$ We find the formal reciprocal, $$\frac{1}{\lambda(z)} = \alpha'(z) \asymp -\frac{6}{z^3} + \frac{6}{5 z} + \frac{79 z}{525} + \frac{116 z^3}{2625} + \frac{91543 z^5}{6063750} + \cdots.$$ Finally we integrate term by term, $$\alpha(z) \asymp \frac{3}{z^2} + \frac{6 \log z }{5} + \frac{79 z^2}{1050} + \frac{29 z^4}{2625} + \frac{91543 z^6}{36382500} + \cdots.$$ and truncate where we like, $$\alpha(z) = \frac{3}{z^2} + \frac{6 \log z }{5} + \frac{79 z^2}{1050} + \frac{29 z^4}{2625} + O(z^6)$$

Numerically, let me give some indication of what happens, in particular to emphasize $ f_{1/2} (\pi/2) = 1.140179\ldots.$

    x      alpha(x)      f(x)       f(f(x))     sin x       f(f(x))- sin x
1.570796   2.089608    1.140179    1.000000    1.000000      1.80442e-11
1.560796   2.089837    1.140095    0.999950    0.999950      1.11629e-09
1.550796   2.090525    1.139841    0.999800    0.999800      1.42091e-10
1.540796   2.091672    1.139419    0.999550    0.999550      3.71042e-10
1.530796   2.093279    1.138828    0.999200    0.999200      1.97844e-10
1.520796   2.095349    1.138070    0.998750    0.998750      -2.82238e-10
1.510796   2.097883    1.137144    0.998201    0.998201      -7.31867e-10
1.500796   2.100884    1.136052    0.997551    0.997551      -1.29813e-09
1.490796   2.104355    1.134794    0.996802    0.996802      -1.14504e-09
1.480796   2.108299    1.133372    0.995953    0.995953      9.09416e-11
1.470796   2.112721    1.131787    0.995004    0.995004      1.57743e-09
1.460796   2.117625    1.130040    0.993956    0.993956      5.63618e-10
1.450796   2.123017    1.128133    0.992809    0.992809      -3.00337e-10
1.440796   2.128902    1.126066    0.991562    0.991562      1.19926e-09
1.430796   2.135285    1.123843    0.990216    0.990216      2.46512e-09
1.420796   2.142174    1.121465    0.988771    0.988771      -2.4357e-10
1.410796   2.149577    1.118932    0.987227    0.987227      -1.01798e-10
1.400796   2.157500    1.116249    0.985585    0.985585      -1.72108e-10
1.390796   2.165952    1.113415    0.983844    0.983844      -2.31266e-10
1.380796   2.174942    1.110434    0.982004    0.982004      -4.08812e-10
1.370796   2.184481    1.107308    0.980067    0.980067      1.02334e-09
1.360796   2.194576    1.104038    0.978031    0.978031      3.59356e-10
1.350796   2.205241    1.100627    0.975897    0.975897      2.36773e-09
1.340796   2.216486    1.097077    0.973666    0.973666      -1.56162e-10
1.330796   2.228323    1.093390    0.971338    0.971338      -5.29822e-11
1.320796   2.240766    1.089569    0.968912    0.968912      8.31102e-10
1.310796   2.253827    1.085616    0.966390    0.966390      -2.91373e-10
1.300796   2.267522    1.081532    0.963771    0.963771      -5.45974e-10
1.290796   2.281865    1.077322    0.961055    0.961055      -1.43066e-10
1.280796   2.296873    1.072986    0.958244    0.958244      -1.58642e-10
1.270796   2.312562    1.068526    0.955336    0.955336      -3.14188e-10
1.260796   2.328950    1.063947    0.952334    0.952334      3.20439e-10
1.250796   2.346055    1.059248    0.949235    0.949235      4.32107e-10
1.240796   2.363898    1.054434    0.946042    0.946042      1.49412e-10
1.230796   2.382498    1.049505    0.942755    0.942755      3.42659e-10
1.220796   2.401878    1.044464    0.939373    0.939373      4.62813e-10
1.210796   2.422059    1.039314    0.935897    0.935897      3.63659e-11
1.200796   2.443066    1.034056    0.932327    0.932327      3.08511e-09
1.190796   2.464924    1.028693    0.928665    0.928665      -8.44918e-10
1.180796   2.487659    1.023226    0.924909    0.924909      6.32892e-10
1.170796   2.511298    1.017658    0.921061    0.921061      -1.80822e-09
1.160796   2.535871    1.011990    0.917121    0.917121      3.02818e-10
1.150796   2.561407    1.006225    0.913089    0.913089      -3.52346e-10
1.140796   2.587938    1.000365    0.908966    0.908966      9.35707e-10
1.130796   2.615498    0.994410    0.904752    0.904752      -2.54345e-10
1.120796   2.644121    0.988364    0.900447    0.900447      -6.20484e-10
1.110796   2.673845    0.982228    0.896052    0.896052      -7.91102e-10
1.100796   2.704708    0.976004    0.891568    0.891568      -1.62699e-09
1.090796   2.736749    0.969693    0.886995    0.886995      -5.2244e-10
1.080796   2.770013    0.963297    0.882333    0.882333      -8.63283e-10
1.070796   2.804543    0.956818    0.877583    0.877583      -2.85301e-10
1.060796   2.840386    0.950258    0.872745    0.872745      -1.30496e-10
1.050796   2.877592    0.943618    0.867819    0.867819      -2.82645e-10
1.040796   2.916212    0.936899    0.862807    0.862807      8.81083e-10
1.030796   2.956300    0.930104    0.857709    0.857709      -7.70554e-10
1.020796   2.997914    0.923233    0.852525    0.852525      1.0091e-09
1.010796   3.041114    0.916288    0.847255    0.847255      -4.96194e-10
1.000796   3.085963    0.909270    0.841901    0.841901      6.71018e-10
0.990796   3.132529    0.902182    0.836463    0.836463      -9.28187e-10
0.980796   3.180880    0.895023    0.830941    0.830941      -1.45774e-10
0.970796   3.231092    0.887796    0.825336    0.825336      1.26379e-09
0.960796   3.283242    0.880502    0.819648    0.819648      -1.84287e-10
0.950796   3.337412    0.873142    0.813878    0.813878      5.84829e-10
0.940796   3.393689    0.865718    0.808028    0.808028      -2.81364e-10
0.930796   3.452165    0.858230    0.802096    0.802096      -1.54149e-10
0.920796   3.512937    0.850679    0.796084    0.796084      -8.29982e-10
0.910796   3.576106    0.843068    0.789992    0.789992      3.00744e-10
0.900796   3.641781    0.835396    0.783822    0.783822      8.10903e-10
0.890796   3.710076    0.827666    0.777573    0.777573      -1.23505e-10
0.880796   3.781111    0.819878    0.771246    0.771246      5.31326e-10
0.870796   3.855015    0.812033    0.764842    0.764842      2.26584e-10
0.860796   3.931924    0.804132    0.758362    0.758362      3.97021e-10
0.850796   4.011981    0.796177    0.751806    0.751806      -7.84946e-10
0.840796   4.095339    0.788168    0.745174    0.745174      -3.03503e-10
0.830796   4.182159    0.780107    0.738469    0.738469      2.63202e-10
0.820796   4.272614    0.771994    0.731689    0.731689      -7.36693e-11
0.810796   4.366886    0.763830    0.724836    0.724836      -1.84604e-10
0.800796   4.465171    0.755616    0.717911    0.717911      3.22084e-10
0.790796   4.567674    0.747354    0.710914    0.710914      -2.93204e-10
0.780796   4.674617    0.739043    0.703845    0.703845      1.58448e-11
0.770796   4.786234    0.730686    0.696707    0.696707      -8.89497e-10
0.760796   4.902777    0.722282    0.689498    0.689498      2.40592e-10
0.750796   5.024513    0.713833    0.682221    0.682221      -3.11017e-10
0.740796   5.151728    0.705339    0.674876    0.674876      7.32554e-10
0.730796   5.284728    0.696801    0.667463    0.667463      -1.73919e-10
0.720796   5.423842    0.688221    0.659983    0.659983      -1.66422e-10
0.710796   5.569419    0.679599    0.652437    0.652437      5.99509e-10
0.700796   5.721838    0.670935    0.644827    0.644827      -2.45424e-10
0.690796   5.881501    0.662231    0.637151    0.637151      -6.29884e-10
0.680796   6.048843    0.653487    0.629412    0.629412      1.86262e-10
0.670796   6.224333    0.644704    0.621610    0.621610      -5.04285e-10
0.660796   6.408471    0.635883    0.613746    0.613746      -6.94697e-12
0.650796   6.601802    0.627025    0.605820    0.605820      -3.81152e-10
0.640796   6.804910    0.618129    0.597834    0.597834      4.10222e-10
0.630796   7.018428    0.609198    0.589788    0.589788      -1.91816e-10
0.620796   7.243040    0.600231    0.581683    0.581683      -4.90592e-10
0.610796   7.479486    0.591230    0.573520    0.573520      4.29742e-10
0.600796   7.728570    0.582195    0.565300    0.565300      -1.38719e-10
0.590796   7.991165    0.573126    0.557023    0.557023      -4.05081e-10
0.580796   8.268218    0.564025    0.548690    0.548690      -5.76379e-10
0.570796   8.560763    0.554892    0.540302    0.540302      1.49155e-10
0.560796   8.869925    0.545728    0.531861    0.531861      1.0459e-11
0.550796   9.196935    0.536533    0.523366    0.523366      -1.15537e-10
0.540796   9.543137    0.527308    0.514819    0.514819      -2.84462e-10
0.530796   9.910004    0.518054    0.506220    0.506220      6.24335e-11
0.520796   10.299155    0.508771    0.497571    0.497571      -9.24078e-12
0.510796   10.712365    0.499460    0.488872    0.488872      8.29491e-11
0.500796   11.151592    0.490122    0.480124    0.480124      3.31769e-10
0.490796   11.618996    0.480757    0.471328    0.471328      2.27307e-10
0.480796   12.116964    0.471366    0.462485    0.462485      3.06434e-10
0.470796   12.648140    0.461949    0.453596    0.453596      4.77846e-11
0.460796   13.215459    0.452507    0.444662    0.444662      1.53162e-10
0.450796   13.822186    0.443041    0.435682    0.435682      -2.87541e-10
0.440796   14.471963    0.433551    0.426660    0.426660      -5.20332e-11
0.430796   15.168860    0.424037    0.417595    0.417595      -8.17951e-11
0.420796   15.917436    0.414501    0.408487    0.408487      -4.6788e-10
0.410796   16.722816    0.404944    0.399340    0.399340      3.70729e-10
0.400796   17.590771    0.395364    0.390152    0.390152      -6.97547e-11
0.390796   18.527825    0.385764    0.380925    0.380925      -2.45522e-10
0.380796   19.541368    0.376143    0.371660    0.371660      4.09758e-10
0.370796   20.639804    0.366503    0.362358    0.362358      1.15221e-10
0.360796   21.832721    0.356843    0.353019    0.353019      -4.75977e-11
0.350796   23.131092    0.347165    0.343646    0.343646      -4.27696e-10
0.340796   24.547531    0.337468    0.334238    0.334238      2.12743e-10
0.330796   26.096586    0.327755    0.324796    0.324796      4.06133e-10
0.320796   27.795115    0.318024    0.315322    0.315322      -2.71476e-10
0.310796   29.662732    0.308276    0.305817    0.305817      -3.74988e-10
0.300796   31.722372    0.298513    0.296281    0.296281      -1.50491e-10
0.290796   34.000986    0.288734    0.286715    0.286715      2.17798e-11
0.280796   36.530413    0.278940    0.277121    0.277121      4.538e-10
0.270796   39.348484    0.269132    0.267499    0.267499      5.24261e-11
0.260796   42.500432    0.259311    0.257850    0.257850      7.03059e-11
0.250796   46.040690    0.249475    0.248175    0.248175      -1.83863e-10
0.240796   50.035239    0.239628    0.238476    0.238476      4.06119e-10
0.230796   54.564668    0.229768    0.228753    0.228753      -2.56253e-10
0.220796   59.728239    0.219896    0.219007    0.219007      -7.32657e-11
0.210796   65.649323    0.210013    0.209239    0.209239      3.43103e-11
0.200796   72.482783    0.200120    0.199450    0.199450      -1.20351e-10
0.190796   80.425131    0.190216    0.189641    0.189641      1.07544e-10
0.180796   89.728726    0.180303    0.179813    0.179813      9.93221e-11
0.170796   100.721954    0.170380    0.169967    0.169967      2.63903e-10
0.160796   113.838454    0.160449    0.160104    0.160104      6.74095e-10
0.150796   129.660347    0.150510    0.150225    0.150225      4.34057e-10
0.140796   148.983681    0.140563    0.140332    0.140332      -2.90965e-11
0.130796   172.920186    0.130610    0.130424    0.130424      4.02502e-10
0.120796   203.060297    0.120649    0.120503    0.120503      -1.85618e-11
0.110796   241.743576    0.110683    0.110570    0.110570      4.2044e-11
0.100796   292.525678    0.100711    0.100626    0.100626      -1.73504e-11
0.090796   361.023855    0.090734    0.090672    0.090672      2.88887e-10
0.080796   456.537044    0.080752    0.080708    0.080708      -2.90848e-10
0.070796   595.371955    0.070767    0.070737    0.070737      4.71103e-10
0.060796   808.285844    0.060778    0.060759    0.060759      -3.90636e-10
0.050796   1159.094719    0.050785    0.050774    0.050774      3.01403e-11
0.040796   1798.677124    0.040791    0.040785    0.040785      3.77092e-10
0.030796   3159.000053    0.030794    0.030791    0.030791      2.4813e-10
0.020796   6931.973789    0.020796    0.020795    0.020795      2.95307e-10
0.010796   25732.234731    0.010796    0.010796    0.010796      1.31774e-10
    x       alpha(x)        f(x)        f(f(x))     sin x       f(f(x))- sin x

Answer 2

This is also a comment. There's another reasonably efficient way to do this sort of computation. Let $L$ be the linear operator on formal power series defined by $L(g) = g(\sin x)$. (Instead of $\sin x$ we could use any formal power series starting with $x$.) Let $I$ be the identity operator, and let $\Delta= L-I$. Then $\Delta$ kills the lowest degree term of its argument, so any infinite sum $\sum_n a_n \Delta^n(g)$ converges as a formal power series. If $\alpha$ is a nonnegative integer then $$L^\alpha(g) = (I+\Delta)^\alpha(g) = \sum_i \binom{\alpha}{i}\Delta^i(g).$$ The coefficient of $x^n$ on the right is a polynomial in $\alpha$ and thus makes sense for any $\alpha$, so we can define $L^\alpha$ for any $\alpha$ by this formula; and we will always have $L^\alpha\circ L^\beta= L^{\alpha+\beta}$. So $f(x) = L^{1/2}(x)$ satisfies $f(f(x)) = \sin x$. Using this approach we can easily compute the coefficients of $f(x)$ up to $x^{100}$ in a few seconds in Maple (though I don't claim that this approach is more efficient than Kevin O'Bryant's).

It might be pointed out this this approach is closely related to the representation of composition of power series as matrix multiplication.

Answer 3

This is more a comment than an answer. The following Mathematica code gave the first 100 coefficients in 44 seconds.

Do[
   f[x_] = Sum[a[k] x^k, {k, 0, exp}];
   term1 = Coefficient[f[f[x]], x, exp];
   term2 = SeriesCoefficient[Sin[x], {x, 0, exp}];
   a[exp] = a[exp] /. First[FindInstance[term1 == term2, a[exp], Rationals]],
 {exp, 0, 100}]
Table[ a[k], {k, 0, 100}]

Here, $f(x) = \sum_{k=0}^\infty a_k x^k$. As expected, $a_{2k}=0$ for $0\leq k \leq 50$, and $a_{2k+1} (2k+2)! 2^{k-1}$ is an integer for $0\leq k \leq 49$.

Here's the list of $a_{2k+1} (2k+2)! 2^{k-1}$ for $0\leq k \leq 22$.

1, 
-2, 
-9, 
-212, 
-9315, 
-556278, 
-25971085, 
4757385496, 
2964298863609, 
1044917608285910, 
215713544372776879, 
-62932769961642167868, 
-98704332065950259333867, 
-30188592688651749114181790, 
58856949571932104601673308075, 
77375921970586388105168106822960, 
-72564223774641266435601127563343119, 
-334464255008553673036506122999946116946, 
-40744061094877107085401232437389280011673, 
2173769171456754713290183664020158569935376220, 
3467462783233757169265913185746537990884591231373,
-21502898790444864584967220140381964189431832253894982,
-93866159932956697746363373697973240405899859356681018397

And here is $\log(|a_k|)$ rounded to the nearest integer for odd $k$ between 0 and 200:

0, -2, -5, -7, -8, -10, -12, -13, -13, -13, -15, -16, -16, -18, -17, 
-18, -19, -18, -21, -18, -19, -19, -19, -19, -18, -20, -18, -19, -17, 
-18, -17, -16, -16, -15, -15, -14, -15, -13, -15, -11, -13, -10, -10, 
-8, -8, -7, -6, -5, -4, -4, -2, -2, 0, -1, 2, 1, 4, 2, 6, 4, 8, 8, 
10, 10, 13, 13, 15, 16, 17, 18, 20, 21, 22, 24, 25, 27, 27, 29, 30, 
32, 33, 35, 35, 38, 38, 41, 39, 44, 43, 47, 47, 50, 50, 53, 54, 57, 
57, 60, 61, 63

That looks to me like super-exponential growth.

Answer 4

Checking the numerators 53,23,92713 (ignoring signs) in the trusty OEIS leads to A048602. Which has references and comments Recursion exists for coefficients, but is too complicated to process without computer algebra system

If you try in the obvious way to compose g with itself when it goes up to $x^{23}$ then you will get terms up to $x^{529}$ all but one of which are useless. Maple has a power series package which allows composition and truncates all terms past the order you specify. I've never used it before now but it looks as if it might be pretty snappy.

update I've removed my terms because others calculated further by better methods. Kevin points out that the largest terms of the first 100 are $a_1=1,a_3=-0.083$ and $a_{99}=0.0231$. 100 seems like a reasonable place to stop, but Gottfreid went further. Unless you click the link to his plots you might miss that (according to him) $a_{255}>10^{48}$. I do think he is correct about the sizes. I thought maybe it was an artifact of calculation but my own modest calculations using Ira's lovely method agree with his (based on a plot) as far as I went which was up to :

[97, -0.011673], [99, 0.023144], [101, 0.83376e-1], [103, -.11914], [105, -.62229], [107, .60156], [109, 4.8816], [111, -2.6819], [113, -40.354], [115, 6.0469], [117, 351.82], [119, 88.156]

Answer 5

This is not a new answer but additional info for Will Jagy's answer about the computation of the Abel-function with the method of J. Écalle.

• [update] With some examples it comes out, that the "standard" computation of the fractional iteration via the formal power series for the iterative logarithm and its truncation to the leading terms provides the same values as Écalle's method using the Abel function as described below. With the same truncation to 64 terms of the power series and the same shift of z_0 to z_h towards zero the difference between the two methods is smaller than 1e-40 , which is the accuracy which is also achieved by each method alone. [end update]

I computed the formal Laurent-series for the Écalle-type Abel-function using Pari/GP to 509 coefficients in exact rational numbers which means the coefficients from $z^{-2}$ to $z^{506}$.

The last coefficient has numerator with 1423 digits and denominator with 1247 digits amounting to an absolute value of about 175 digits, roughly -2.66945040282 E175 , so the series has in the same way as the comparable series for the fractional iteration of $\exp(x)-1$ zero-radius of convergence and when we plot the curve showing the number of digits of the nonzero coefficients by $\log_{10}(|a_k|)$ we get the typical shape of the upright hockeystick.

Here are the leading 11 nonzero terms of the Laurent series for the Abel-function (which I call here "incomplete Abel function" so far because the "complete" Abel-function needs also the term for the logarithm and the term for the iteration-height h (this is index n in Will's answer):

  Laurent-series in z:                             3  *z^-2
                                           + 79/1050  *z^2
                                           + 29/2625  *z^4
                                    + 91543/36382500  *z^6
                              + 18222899/28378350000  *z^8
                             + 88627739/573024375000  *z^10
                        + 3899439883/142468185234375  *z^12
              - 32544553328689/116721334798818750000  *z^14
                 - 4104258052789/1554729734250000000  *z^16
 - 119345896838809094501/141343700374629565312500000  *z^18
      + 745223773943295679/3505548124370772949218750  *z^20
             + O(z^22)

$ \qquad \qquad$ (remark: see an overview characterizing the growthrate at end (§2))

This gives the "incomplete Abel function" in terms of its coeffs up to some truncation n (all formulae in Pari/GP notation):

 abel_inc(z,n=64) = sum(k=1,n, coeff[k]*z^(k-3) )     

The complete Abel-function is then :

 {abel(z,h=32,n=64) = local(z_h,a); \\ give some sufficient default values 
                                    \\ in h and n for the required numerical 
                                    \\ precision of the approximate results
        z_h = sin_iter(z,h);        \\ sin_iter prev. defined as iterable sin()
      a = abel_inc(z_h,n) + 6/5*log(z_h) - h ;
      return(a); }                      

The inverse abel-function must be implemented by some root-solver. In Pari/GP I used the following, where the inverse Abel-function is included in the body of the full fractionally-iterable sin_h() function:

    {sin_h (h = 0,z_0=1) = local(a_0,z_h,a_h);  \\ restriction abs(h)<1 
               a_0 = abel(z_0, 32, 64);         \\ get the Abel-value for z_0
                                                \\ with meaningful precision
               a_h = a_0 + h ;                  \\ comp Abel-value for z_h
                                 \\ the following is the implementation of
                                 \\ the inverse Abel-function:
         z_h = solve(z = sin(z_0),z_0, abel(z,32,64) - a_h);
         return(z_h); }

The following is done to apply the above to some example, reproducing additivity of the iteration heights 0.5 and 0.5 to integral height 1 with more than 40 digits precision:

                               \\  Pari-output
   z_0  = 1                    \\  %529 = 1
   z_05 = sin_h(0.5,z_0 )      \\  %530 = 0.908708429743
   z_1  = sin_h(0.5,z_05)      \\  %531 = 0.841470984808
   z_1 - sin(z_0)              \\  %532 = -6.38920219348 E-42

Below I show the recomputed list of computations in Will's answer with 40 digits correct:

   step   z0=Pi/2 - step   abel(z0)   z05=sin_h(0.5,z0) z1=sin_h(0.5,z05)  z1 - sin(z0)
   0.00   1.57079632679  2.08962271973   1.14017947617  1.00000000000   -2.89445031739E-41
   0.05   1.52079632679  2.09536408453   1.13806963935  0.998750260395  -2.86591796888E-41
   0.10   1.47079632679  2.11273622895   1.13178674818  0.995004165278  -2.78164697945E-41
   0.15   1.42079632679  2.14218948912   1.12146458427  0.988771077936  -2.64553725829E-41
   0.20   1.37079632679  2.18449553252   1.10730765183  0.980066577841  -2.46383393292E-41
   0.25   1.32079632679  2.24078077607   1.08956885996  0.968912421711  -2.24476553049E-41
   0.30   1.27079632679  2.31257688904   1.06852649593  0.955336489126  -1.99807394218E-41
   0.35   1.22079632679  2.40189260763   1.04446448663  0.939372712847  -1.73446474837E-41
   0.40   1.17079632679  2.51131312355   1.01765794736  0.921060994003  -1.46500647333E-41
   0.45   1.12079632679  2.64413616528  0.988364216777  0.900447102353  -1.20050550750E-41
   0.50   1.07079632679  2.80455803137  0.956818478819  0.877582561890  -9.50882282773E-42
   0.55   1.02079632679  2.99792899241  0.923232674366  0.852524522060  -7.24576289372E-42
   0.60  0.970796326795  3.23110684637  0.887796468526  0.825335614910  -5.28014362671E-42
   0.65  0.920796326795  3.51295197372  0.850679308887  0.796083798549  -3.65188391373E-42
   0.70  0.870796326795  3.85503037983  0.812032915560  0.764842187284  -2.37402622132E-42
   0.75  0.820796326795  4.27262886030  0.771993802047  0.731688868874  -1.43260703471E-42
   0.80  0.770796326795  4.78624925852  0.730685613103  0.696706709347  -7.89576195851E-43
   0.85  0.720796326795  5.42385666222  0.688221187210  0.659983145885  -3.89074331205E-43
   0.90  0.670796326795  6.22434753781  0.644704322722  0.621609968271  -1.66626510284E-43
   0.95  0.620796326795  7.24305478745  0.600231264287  0.581683089464  -5.96979699941E-44
   1.00  0.570796326795  8.56077779381  0.554891942675  0.540302305868  -1.69831000319E-44

A picture of $y=\sin(x)$, the half-iterate $y=\sin^{\circ 0.5}(x)$ , $y=\sin^{\circ 1/3}(x)$ and $y=x$:

Remark: at x, where sin(x)=0 the computation of the Abel-function runs in singularities and the value for the function is (interpolated from its neighbourhood) assumed to be zero.

---

In the Abel-function abel(z,h=32,n=64)=... there is the parameter h which allows to control the quality of approximation. The formal exact solution is given as limit when h goes to infinity - but we use only finite approximations here. They key is, that h controls the implicite iteration of the argument z towards the fixpoint zero, so the numerical evaluation of the (truncated to n coefficients) Laurent-series gives a better approximation to the true value - although actually the convergence-radius is still zero! The purpose of those iterations shifting z_h towards zero is to shift the position, from where the Laurent series with the argument z_h begins to diverge, to higher indexes and thus to get more accuracy. A combination of h=32 and n=64 for arguments $|z| \le 1$ is apparently enough for 40 correct digits. (see remark (§1))

Finally, to show the effect of the h=32 iteration at work I provide below the partial sums of the Laurent-series for z=1 in comparision to h=4.

In the first example I use h=4 and in the second example I use h=32 .
In the table k is the index of the coefficient up to where the partial sums are computed. ps_k indicates the partial sum using z_h which is the h 'th iterate from z_0=1 . But for convenience the term for the logarithm and the h-term are always included so we can compare the sum up to this term with the accurate value a_1 for the Abel-function at z_1 :

   k    ps_k              error:  a_1 - ps_k    iteration height h=4
   0  3.05810608515        -0.0315166345810
   2  3.05810608515        -0.0315166345810
   4  3.08773833843       -0.00188438129901
   6  3.08945198975      -0.000170729978211
   8  3.08960570369     -0.0000170160371392
  10  3.08962115403    -0.00000156570332243
  12  3.08962261968   -0.000000100050871450
  14  3.08962272183  0.00000000210083986271
  16  3.08962272142  0.00000000169099804938
  18  3.08962271989       1.62746538183E-10
  20  3.08962271970      -2.97721970306E-11
  ... 
  50  3.08962271973      -3.98604755990E-18
  52  3.08962271973       7.74229820435E-19
  54  3.08962271973       1.21098784690E-18
  56  3.08962271973      -6.22150631919E-20
  58  3.08962271973      -3.98357488277E-19
  60  3.08962271973      -3.38541477910E-20
  62  3.08962271973       1.42850133024E-19

We see, that with iteration-height h=4 we arrive at an absolute error smaller than 1e-18 at the 64. term. And below, iteration-height h=32 provides accuracy to an absolute error of smaller than 1e-40 with that 64 terms used:

   k    ps_k              error:  a_1 - ps_k    iteration height h=32
   0  3.08337725463         -0.00624546510435
   2  3.08337725463         -0.00624546510435
   4  3.08954701281       -0.0000757069234782
   6  3.08962130264      -0.00000141708899538
   8  3.08962269011    -0.0000000296188288642
  10  3.08962271915  -0.000000000581829933894
  12  3.08962271972        -8.31025344698E-12
  ... ...                  ...
  52  3.08962271973        -3.06907747463E-37
  54  3.08962271973         5.27409063179E-37
  56  3.08962271973         2.10119895640E-38
  58  3.08962271973        -6.82487772781E-39
  60  3.08962271973        -5.39925105785E-40
  62  3.08962271973         9.44571568505E-41

---

(§1): a Noerlund-summation, as I have it proposed in some treatizes for the evaluation of the fractional iterates of the $\exp(x)-1$ might give arbitrary approximations as well, but it seems now to me that such a summation-procedure were at most needed here for theoretical reasons to prove the summability of the Laurent-series for the Abel-function.

(§2): A short overview over the first 512 coefficients of the abel_inc()-series:

 index      value             index   value            index    value               index    value
    0           3.000000000   47                     0   92       -0.005185699555  496       4.633504372E168 
    1                     0   48  -0.00000003870320993   93                     0  497                     0
    2                     0   49                     0   94         0.01347223160  498      -4.983759375E169
    3                     0   50  0.000000006386371562   95                     0  499                     0
    4         0.07523809524   51                     0   96         0.03559427183  500      -8.187596780E170
    5                     0   52   0.00000006229599636   97                     0  501                     0
    6         0.01104761905   53                     0   98        -0.06747379661  502       8.333103850E171
    7                     0   54   0.00000001451248843   99                     0  503                     0
    8        0.002516127259   55                     0  100         -0.2528544049  504       1.467790435E173
    9                     0   56   -0.0000001074166810  101                     0  505                     0
   10       0.0006421408926   57                     0  102          0.3439480705  506      -1.412786474E174
   11                     0   58  -0.00000007200630916  103                     0  507                     0
   12       0.0001546666126   59                     0  104           1.879638019  508      -2.669450403E175
   13                     0   60    0.0000001982539503  105                     0  ...          ...
   14      0.00002737060121   61                     0  106          -1.706858981
   15                     0   62    0.0000002440284845  107                     0
   16   -0.0000002788226624   63                     0  108          -14.69827943
   17                     0   64   -0.0000003845753696  109                     0
   18    -0.000002639853064   65                     0  110           7.295584305
   19                     0   66   -0.0000007917263057  ...             ...         
   20   -0.0000008443665796   67                     0
   ...                  ...   ...                  ...

Answer 6

Another helping comment: There is a general statement about the convergence radius of fractional iterates developed at a fixed point with multiplier 1:

The set of values $\lambda$ for which the regular iteration formal powerseries $f^\lambda$ has non-zero convergence radius is either: (1) only $\lambda=0$ (2) the points $k\lambda_0$, $k\in\mathbb{Z}$, for one $\lambda_0\in\mathbb{C}$. Example $e^z-1$ with $\lambda_0=1$. (3) the whole complex plane. Example $\frac{z}{1-z}$.

This result is due to Écalle [1] and preliminary work of Baker [2]. In our case the original function $\sin(x)$ has non-zero convergence radius, and hence all its integer iterations too. So it may only occur case (2) with $\lambda_0=\frac{1}{n}$ for some integer $n$ or case (3). My conjecture is case (2) with $\lambda_0=1$, but the particular proof needs to be done, (like Baker did it for $e^x-1$)

[1] Écalle, J. (1973). Nature du groupe des ordres d’itération complexes d’une transformation holomorphe au voisinage d’un point fixe de multiplicateur 1. C. R. Acad. Sci., Paris, Sér. A, 276, 261–263.

[2] Baker, I. N. (1962). Permutable power series and regular iteration. J. Aust. Math. Soc., 2, 265–294.

Answer 7

If you create the Bell-matrix for the function $f(x) = \sin(x)$, say SI, then you can compute the matrix-logarithm of SI, say SIL = MLog(SI). Then a formal power of SI is SIP(h) = MExp(h*SIL) and the Bell-matrix for the height-dependend function $ \operatorname{sin\_iter}(x,h)$, which has polynomials in h for the coefficients at x . SI begins with

  1        .     .       .
  0        1     .       .
  0        0     1       .
  0     -1/6     0       1
  0        0  -1/3       0
  0    1/120     0    -1/2
  0        0  2/45       0
  0  -1/5040     0  13/120

where column 1 contains the coefficients for the power series $\sin(x)$, column 2 that for $(\sin(x))^2$, column 0 that for $(\sin(x))^0 = 1$ and similarly for all other columns k.

The matrix-logarithm SIL begins with

  0         .      .      .     .     .  .  . 
  0         0      .      .     .     .  .  . 
  0         0      0      .     .     .  .  . 
  0      -1/6      0      0     .     .  .  . 
  0         0   -1/3      0     0     .  .  . 
  0     -1/30      0   -1/2     0     0  .  . 
  0         0  -1/15      0  -2/3     0  0  . 
  0  -41/3780      0  -1/10     0  -5/6  0  0 

Here the column k is the k'th multiple of column 1 shifted $k-1$ row downwards.

Then column 1 of SIP(h) = MExp(h*SIL) is

                              0
                              1
                              0
                         -1/6*h
                              0
                1/24*h^2-1/30*h
                              0
  -5/432*h^3+1/45*h^2-41/3780*h

and the function $\operatorname{sin\_iter}$ is

$$ \operatorname{sin\_iter}(x,h) = 1 x - h \cdot {x^3 \over 3!} + (5 h^2-4 h) \cdot {x^5 \over 5!} - (...) \cdot {x^7 \over 7!} + O(x^9) $$

Inserting $h={1 \over 2}$ gives you the powerseries for the half-iterate.

Using 64 terms it looks as if the radius of convergence for $h=\frac 12$ will be 1, since the absolute values of the coefficients seem to stabilize to the interval $ \pm 1E-7 $ but I'll look at this further later this day.

[Update]

using 256 terms there occurs a clear growthrate of the coefficients. Looking at the log of absolute values of that coefficients we get a rough impression. See here:

http://go.helms-net.de/math/images/sincoeff_c.png

These are the coefficients at $x^{123},x^{125},x^{127}$ and $x^{251}, x^{253}, x^{255}$:

c_123     -2156.72733764089915  // 4 digits
c_125     31313.42875545542423  // 5 digits
c_127     34859.64557727596911  // 5 digits 
...    
c_251       -35365220492708296140377087748804440170254492009.570  // 46 digits    
c_253     -1378449672866233726070664896135098313484573633108.4    // 48 digits    
c_255       987848122496441964413343332623221752473112662017.00   // 47 digits    

Differences of the logs are also quotients of the coefficients By the plot of the differences we get also a trend of logarithmic increase. (If the differences continue to increase then the radius of convergence of the powerseries is zero, because the growthrate of the absolute values of the coefficients is hypergeometric)

http://go.helms-net.de/math/images/sincoeff_d.png

[end update]

Pari/GP computes this pretty fast, it took,let say 5 seconds to handle 64-term-matrices.

[update2 , Feb 2016]
A very simple method to get the formal powerseries for the half-iterate for the sine-function is combining the Pari/GP-internal taylor-expansion-function, the serreverse() function with the Newton_algorithm for the squareroot. For a scalar $t$ as root of a given $z$ is $t_{k+1}=(z/t_k+t_k)/2$ and here we interpret $t$ and $z$ as powerseries, where $t$ is also invertible.
Here is the protocol of the Pari/GP-session:

t=x + O(x^12)   \\ Initialization of the Newton-algorithm with a simple power series
 %76 = x + O(x^12)  \\ the protocol that Pari/GP shows in the dialog

t = (sin(serreverse(t))+t)/2   \\ first iteration
 %77 = x - 1/12*x^3 + 1/240*x^5 - 1/10080*x^7 + 1/725760*x^9 - 1/79833600*x^11 + O(x^12)

t = (sin(serreverse(t))+t)/2   \\ secons iteration
 %78 = x - 1/12*x^3 - 1/160*x^5 - 11/5040*x^7 - 11/17920*x^9 - 2425/12773376*x^11 + O(x^12)

t = (sin(serreverse(t))+t)/2
 %79 = x - 1/12*x^3 - 1/160*x^5 - 53/40320*x^7 - 341/1935360*x^9 + 44311/638668800*x^11 + O(x^12)

t = (sin(serreverse(t))+t)/2
 %80 = x - 1/12*x^3 - 1/160*x^5 - 53/40320*x^7 - 23/71680*x^9 - 138913/1277337600*x^11 + O(x^12)

t = (sin(serreverse(t))+t)/2
 %81 = x - 1/12*x^3 - 1/160*x^5 - 53/40320*x^7 - 23/71680*x^9 - 92713/1277337600*x^11 + O(x^12)

t = (sin(serreverse(t))+t)/2  
 %82 = x - 1/12*x^3 - 1/160*x^5 - 53/40320*x^7 - 23/71680*x^9 - 92713/1277337600*x^11 + O(x^12) // the solution becomes stable for the first coefficients

The coefficients can be extended very simple to an arbitrary index, just set the default power series expansion to desired precision and define the initialization of t accordingly.

Answer 8

(This should go as a comment, but was impossible.) @Aaaron: I've uploaded a list of the first 128 nonzero coefficients, see:

https://go.helms-net.de/math/tables/sinxcoeffs.htm

Also here is a routine for Pari/GP to compute the sqrt of a lower triangular Bell-matrix (the matrix SI in my earlier answer) With this you can compute the powerseries for the half-iterate (by column 1 of sqrt of SI) in a second even if the matrix size is 256x256.

\\ square-root of a lower triangular Bell-matrix
\\ only implemented for operator/"Bell"-matrices for functions
\\ where f(x) = ax  + bx^2+ cx^3 + ... with a>0
\\
 trisqrt(m) = local(tmp, rs=rows(m), cs=cols(m), c);
  tmp=matrix(rs,cs,r,c,if(r==c,sqrt(m[r,r])));
  for(d=1,rs-1,
       for(r=d+1,rs,
          c=r-d;
          tmp[r,c]=(m[r,c]-sum(k=c+1,r-1, tmp[r,k]*tmp[k,c]) )/(tmp[c,c]+tmp[r,r])
          );
      );
 return(tmp);