It appears that there are some related questions on this forum. For example,
However, someone usually emphasizes a single invariant and its relationship with graph isomorphism, such as the spectrum.
What I want to ask is whether, if one invariant cannot determine it, we hope in combining multiple invariants, such as chromatic number, matching number, the number of orbits in the automorphism group, and so on. In other words, is there hope that the combination of invariants can achieve this? Common invariants can be found in the The House of Graphs
, and we have included a screenshot below.
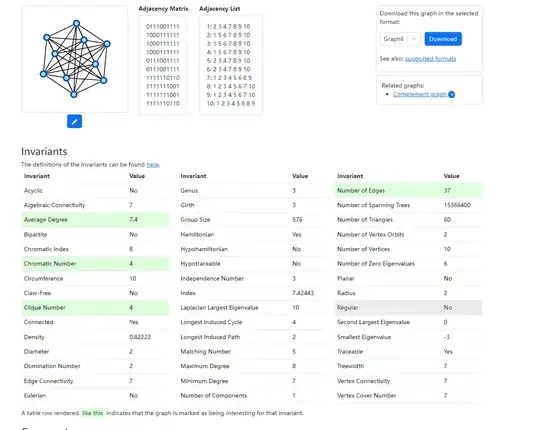
How many invariants do we need to combine in order to determine whether two graphs are isomorphic? Or is this idea directly negative from the start? With the listed 40+ invariants from the screenshot, if they are all the same, is it possible to find two non-isomorphic graphs?