Covering unit-radius balls with unit-diameter objects

Question

Let $d$ be a norm-based metric in $\mathbb{R}^2$. We are given a $d$-ball with radius 1, and we would like to cover it with objects with diameter 1. How many objects are needed?

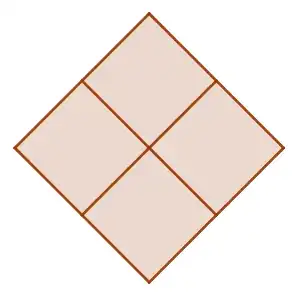
In the $\ell_1$ metric, 4 are sufficient (and probably necessary):

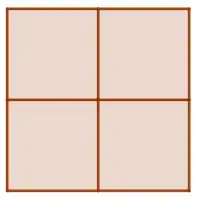
Similarly, in the $\ell_\infty$ metric, 4 are sufficient (and probably necessary):

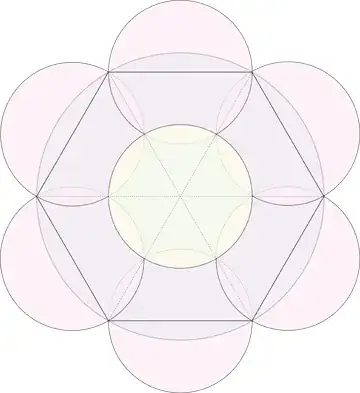
In the $\ell_2$ metric, 7 are sufficient, according to this answer by Joseph O'Rourke:

For covering with disks, 7 are also necessary (it cannot be covered by 6 disks), but maybe it can be covered by other objects with diameter 1.

QUESTION: is there a finite integer $C$ such that, for every metric $d$, every $d$-ball of radius 1 can be covered by $C$ objects of diameter 1?

NOTE: the following related questions are interesting too:

is there a finite integer $B$ such that, for every metric $d$, every $d$-ball of radius 1 can be covered by $B$ $d$-balls of diameter 1?
is there a finite integer $A$ such that, for every metric $d$, every $d$-ball of radius 1 can be covered by $A$ $d$-balls of radius $1/2$?

It is easy to see that $C\leq B\leq A$ (the latter follows from the fact that each $d$-ball of radius $1/2$ has diameter at most $1$ by the triangle equality).

EDIT 1: Anton Petrunin showed that $A$ is finite (and therefore $B$ and $C$ are finite too). A followup question is: what are tight upper bounds on these numbers?

I conjecture that $A\leq 16$: we can take the unit ball and apply an affinte transformation on it such that it contains a unit square, and is contained in a square of side-length at most 2 (I am not sure about the 2, but it holds for a triangle, and triangle seems a worst-case for all convex figures). Therefore, we can cover the unit ball by $4\times 4$ squares of side-length $1/2$; each of these is contained in a ball of radius $1/2$. Is the conjecture true? Is it possible to get tighter upper bounds on $A, B$ or $C$?

EDIT 2: in this paper we prove an upper bound $A\leq 25$, as well as motivate the search for tighter bounds: it provides a constant-factor approximation to an NP-hard matching problem.

Does the question ask whether, for some fixed type of object, we can do it, or for every fixed choice of object, we can do it, or does it allow that the type of object depends on the metric? — LSpice, Dec 12 '22 at 21:22
@LSpice the type of object can depend on the metric. It can be any object with diameter 1 in that metric. — Erel Segal-Halevi, Dec 13 '22 at 09:01
To cover the Euclidean unit disc with 6 objects of diameter 1, divide it into 60-degree sectors. — Noam D. Elkies, Dec 21 '22 at 19:59
@NoamD.Elkies Thanks! This already shows that $C<B$ is possible. — Erel Segal-Halevi, Dec 26 '22 at 08:16

score 2 · Accepted Answer · answered Dec 12 '22 at 17:06

2

I assume you mean all metrics induced by norm, otherwise the answer is obviously "no".

For any norm there is a bilipschitz euclidean norm with coefficient $\le 10$. Note that a unit ball in the euclidean plane can be covered $100000000$ balls of radius $\tfrac1{100}$. Whence $C= 100000000$ will do.

answered Dec 12 '22 at 17:06

Anton Petrunin

43,739

Shouldn't the small balls have diameter $\frac{1}{100}$, instead of radius $\frac{1}{100}$? – Saúl RM Dec 12 '22 at 17:47
"For any norm there is a bilipschitz euclidean norm with coefficient ≤10" I did not understand this sentence. Can you give a reference where I can read more about this theorem? – Erel Segal-Halevi Dec 12 '22 at 18:15
@ErelSegal-Halevi Use the norm induced by Johnson's ellipsoid. – Anton Petrunin Dec 12 '22 at 22:17
@SaúlRM, yeah, maybe some constants should be changed :) – Anton Petrunin Dec 12 '22 at 22:18
1

@ErelSegal-Halevi In case it is helpful: remember that there is a bijection between norms in $\mathbb{R}^n$ and compact convex neighborhoods $K$ of $0$ with $K=-K$ ($K$ is the ball $B(0,1)$ in some norm). Moreover, if the ball is an ellipsoid, then the problem is the same as the problem with Euclidean balls, because an ellipsoid (in $\mathbb{R}^2$, an ellipse) is an affine image of the sphere. Also, for any convex $K$ in $\mathbb{R}^2$ generating a norm, its Outer John ellipsoid (see wikipedia) contains $K$ and is contained in $2K$, so their norms are $2$-Lipschitz respect to each other. – Saúl RM Dec 12 '22 at 22:45
@SaúlRM what do you mean by "convex K in R2 generating a norm" - how exactly does K generate a norm? (sorry if this is too obvious) – Erel Segal-Halevi Dec 15 '22 at 07:13
1

@ErelSegal-Halevi by the norm generated by a compact, convex, balanced set I just mean its Minkowski functional. For a reference on why they generate norms see for example theorem 1.39 of Rudin's $\textit{Functional Analysis}$ – Saúl RM Dec 15 '22 at 08:13

Covering unit-radius balls with unit-diameter objects

1 Answers1