Here is a key question (i.e., Question 2 below) that, if correctly answered, would let me support a very general conjecture on a wide class of related problems, a conjecture that I have never shared before.
In the Euclidean space $\ \mathbb{R}^3,\ $ let
$$ \mathcal H(4,3)\ :=\ \{0,1,2,3\}\times\{0,1,2,3\}\times\{0,1,2,3\} \,\ \subseteq\,\ \mathbb R^3 $$
We consider the family of all the distinct straight lines that joins at least two elements of $\mathcal{H}(4,3)$ (i.e., we need to take into account all the lines that pass through two distinct points among the $64$ given elements of the above mentioned cubic lattice).
Now, let us call $\mathcal{I_2}(4,3):=\{S_1,S_2, \dots, S_{t-1}\, S_t\}$ the set of all the (distinct) intesections of the family of lines above.
Question 1: Which is $t$, the cardinality of $\mathcal{I_2}(4,3)$?
Question 2: If we check by brute force all the possible polygonal chains consisting of $21$ or $22$ line segments (how many?), whose vertices always belong to $\mathcal{I_2}$, will we find at least one covering trail for $\mathcal{H}(4,3)$ (i.e., is it possible to draw at most $22$ consecutive links starting and ending on the vertices of $\mathcal{I_2}$ and joining in this way all the $64$ elements of the set $\mathcal{H}(4,3)$?)?
Current results: I have showed that we can constructively solve the problem by Question $2$ with a polygonal chain of length $23$ or less,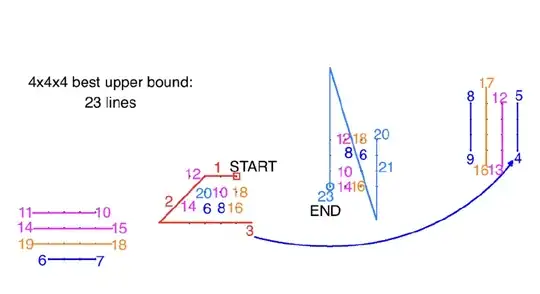 
$23$ lines" /> whereas it is not possible to find any solution spending less than $21$ lines (trivial lower bound)1.
By improving my current upper bound, I would finally be able to strongly conjecture that the link length of any minimum-link covering trail for any set of $\{0,1,2,\dots,n-1\}\times\{0,1,2,\dots,n-1\} \times \dots \times\{0,1,2,\dots,n-1\}$ in $\mathbb{R}^k$ is equal to $\frac{n^k-1}{n-1}+n-3$ (here we are assuming that $n \in \mathbb{N}-\{0,1,2\}$ and $k \in \mathbb{N}-\{0,1\}$).
Otherwise, if we will be able to show that it is not possible to improve my upper bound of $23$ lines, I would infer that the general solution for the $\{0,1,2,\dots,n-1\}\times\{0,1,2,\dots,n-1\}\times \dots \times\{0,1,2,\dots,n-1\}\subset \mathbb{R}^k$ points problem is given by $\frac{n^k-1}{n-1}+(k-1)\cdot(n-3)$.
I am persuaded that the $22$ lines solution is likely to exist (or at least I strongly believe that it does not exist any covering trail consisting of only $21$ links that covers $\mathcal{H}(4,3)$), but I would not have many arguments to support my general claim without confirming the above by brute force testing.
Moreover, I have constructively proven that the link-length of the optimal covering trail for the set $\{0,1,2,3,4\}\times\{0,1,2,3,4\}\times\{0,1,2,3,4\} \subset \mathbb{R}^3$ belongs to $\{31, 32, 33, 34, 35, 36\}$, see the figure below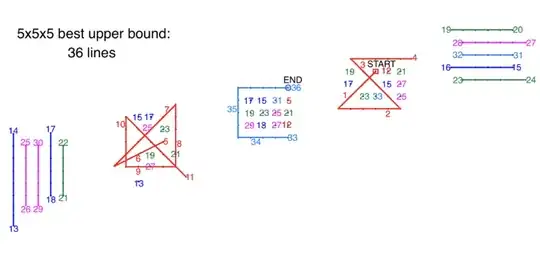 
2.
Related OEIS sequence: A318165.
P.S. It is trivial to point out that all the $S_i$, for any $i=1,2,...,t$, necessarily belong to the Axis-Aligned Bounding Box $[-6,9] \times [-6,9] \times [-6,9]$.
Some useful References concerning the general problem:
1 - Proved untrivial bounds for the general problem) S. Bereg, P. Bose, A. Dumitrescu, F. Hurtado, and P. Valtr. Traversing a set of points with a minimum number of turns. Discrete & Computational Geometry, 41(4):513–532, 2009.
2 - Proof that my general conjecture holds for $k=2$) B. Keszegh. Covering paths and trees for planar grids. Geombinatorics Quarterly, 24(1):5–10, 2014.
3 - General problem under some simplifying constraints) E. Kranakis, D. Krizanc, and L. Meertens. Link length of rectilinear Hamiltonian tours in grids. Ars Combinatoria, 38:177–192, 1994.
4 - Conjectures in conclusion) M. Ripà, Minimum-Link Covering Trails for any Hypercubic Lattice, arXiv, 2022.
5 - Proof that my general conjecture holds for $n=3$) M. Ripà. Solving the 106 years old 3k points problem with the clockwise-algorithm. Journal of Fundamental Mathematics and Applications, 3(2):84–97, 2020.
Announcement) We have also proven that it is possible to solve the general case ($n=2, k=k$) with exactly $3 \cdot 2^{k-2}$ lines and the full paper will be released in a couple of weeks.
The proof that the trivial lower bound $h(n,k) \geq \frac{n^k-1}{n-1}$ holds for every $n,k \in \mathbb{N}-{0,1,2}$ follows as a special case of Theorem 2.1 here: https://arxiv.org/pdf/2208.01699.pdf .
Therefore, as far as I know, the current bound is still $21 \leq h(4,3) \leq 23$.
– Marco Ripà Jan 21 '24 at 16:58