So I was messing around with Bernoulli numbers and values of $\zeta'$ at integers $-$ and suddenly I came about a non trivial identity which can be written in terms of the logarithmic derivative of the zeta function, $z(x):=\frac{\zeta'(x)}{\zeta(x)}$.
This is the kind of identities I would have typically expected to find, maybe in some variation, on the Wolfram functions site, but I didn't. It states:
$$z(n)-z(n-2)+z(1-n)-z(3-n)+\frac1{n-1}+\frac1{n-2}=0.$$
The intriguing part are of course the two fractions.
This identity seems to hold not only for positive even $n$, but for random complex numbers as well, except obviously the points where one of the zeta values is $0$.
There are several ways to write it as a reflection formula. The most simple and beautiful one, as for me, is as follows (replacing $n$ by $x+1$): if we define a function $$f(x):=\frac{\zeta'(x+1)}{\zeta(x+1)}-\frac{\zeta'(x-1)}{\zeta(x-1)}+\frac1{x},$$
then the identity simply becomes $$f(x)=f(1-x),$$ as also illustrated by the graph. 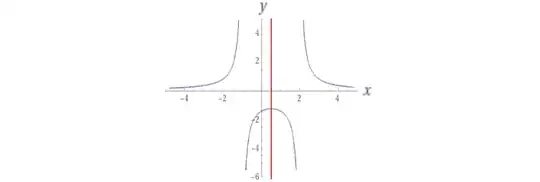 I just cannot believe this result should be new...
I just cannot believe this result should be new...
Something about motivation: I noticed the occurring of expressions of the type $\color{red}{z(n)-z(n-2)}$ (always with even $n\in\mathbb N$) in closed forms of integrals like this one: $$\int_{0}^{\infty}\frac{1}{e^x-1}\left[\frac{12\,e^x}{(e^x-1)^2}-\frac{12}{x^2}+1\right]\,dx=\frac{5}{2}+\color{red}{\frac{\zeta'(2)}{\zeta(2)}-\frac{\zeta'(0)}{\zeta(0)}}$$ and this one: $$ \int\limits_0^\infty\dfrac{\tanh^3(x)}{x^2}dx=\frac{5}{6} - \frac{4}{15} \log 2 + \color{red}{\frac{\zeta'(4)}{\zeta(4)} -\frac{\zeta'(2)}{\zeta(2)}},$$ which further had lead me to $$\int\limits_0^\infty\dfrac{\tanh^5(x)}{x^2}dx= \frac{8}{15}-\frac{44}{189}\log2 + \color{red}{\frac{\zeta'(4)}{\zeta(4)} -\frac{\zeta'(2)}{\zeta(2)}} -\frac23\Bigl(\color{red}{\frac{\zeta'(6)}{\zeta(6)}-\frac{\zeta'(4)}{\zeta(4)}} \Bigr) $$ etc.