 I have been experimenting with number theoretic techniques to get some algorithmic compositions. I use python (mingus) to create the midi, import it on musescore 2 and have the corresponing score.
I have been experimenting with number theoretic techniques to get some algorithmic compositions. I use python (mingus) to create the midi, import it on musescore 2 and have the corresponing score.
The method is based on a few ingredients:
I use C-major or C-minor and use a symmetric function $f(a,b,c,\cdots)$ and plug in numbers $a,b,c,$ from $1 \le x \le 31$ or some other intervall and compute $f(a,b,c,..) \mod 8$ or $\mod 5$ to generate the pitches.
To generate the rhythms / bars, I use a technique to map natural numbers to binary trees (divisorTree, sumTree). This way I have some control over the rhythm fast / slow by plugging in different numbers.
In a mixed ensemble I use binary digits to determine at which bar the instrument plays. This creates attention to the listener, so that he/she asks himself/herself, what comes next.
Which other algortihmic techniques from number theory do you know which are used for algorithmic compositions?
Thanks for your help.
The scores can be found at: https://musescore.com/user/37663311
Edit: I use e new technique to create a piece of 48 min with 8 instruments and 650 pages scores: (I hope you enjoy:)
https://musescore.com/user/37663311/scores/6651858
Another edit: Voronoi diagram / Delaunay triangulation of pitch consonance similarity, as measured with the kernel $k(a,b) = \frac{\gcd(a,b)^2}{ab}$:
https://www.reddit.com/r/musictheory/comments/tcamot/an_image_of_pitches_for_pitch_consonance/
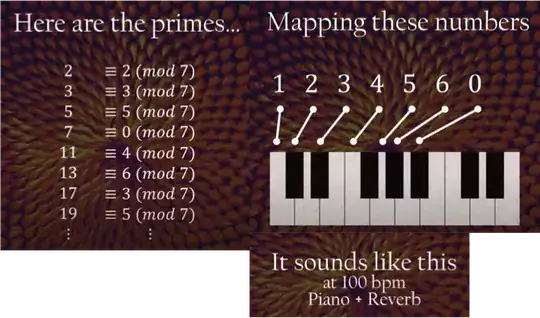

 (the second and third of these compositions combine the number theory input in the right hand with human derived chords in the left hand; apologies for the advertisement one needs to click through in order to hear the composition)
(the second and third of these compositions combine the number theory input in the right hand with human derived chords in the left hand; apologies for the advertisement one needs to click through in order to hear the composition)
The "number theory" is mostly arithmetic mod 12, and related mathematical artifacts such as the 24-element dihedral group. – Noam D. Elkies Mar 06 '21 at 16:06