21

An animal in the plane is a finite set of grid-aligned unit squares in $\mathbb{R}^2$. (The definition is the same as a polyomino, but where we relax the connectivity requirement.) One may equivalently think of them as finite subsets of $\mathbb{Z}^2$.

In Erich Friedman’s investigation of tilings of rectangles by 1D animals, it is mentioned offhandedly that Coppersmith showed every 4-celled animal tiles the plane in 1985 (and can do so without reflections); I was able to locate the paper at Coppersmith - Each four-celled animal tiles the plane (link to PDF). 6-celled animals do not, in general, since they can have a hole:

6-celled animal with hole

Has any progress been made on the 5-cell case since 1985 (either with or without reflections permitted)? I'd be interested in computational results as well, e.g. "every size-5 subset of a $7\times 7$ grid tiles the plane". (I have confirmed that every size-5 subset of a $3\times 3$ grid tiles the plane, and every size-5 subset of a $4\times 4$ grid at least covers a $10\times 10$ square.)

Since I realize the answer to this question may well be "no further progress has been made and the problem is difficult", I'm interested in any statements that can be made about restrictions of this problem to natural subcases. For instance:

  • Can every size-5 subset of $\mathbb{Z}$ tile the plane? Of $\mathbb{Z}\times \{0,1\}$?

  • I didn't specify above, but one can consider whether reflections are allowed in a tiling or not. If so, a proof may be easier (it seems Coppersmith restricted himself to the rotation case), and if not, a counterexample might be more tractable.

  • Is there expert consensus on what the likely answer is?

Previously on math.SE here, without any progress on the question.

Edit 2021-05-04: I contacted Dr. Coppersmith about the problem, and he wasn't aware of any further research in this direction.

RavenclawPrefect
  • 2,298
  • At this writing, there is still an active bounty on the question at m.se. – Gerry Myerson Jan 05 '21 at 22:27
  • I drafted this post when the bounty was almost over, anticipating no further answers, and accidentally posted it here earlier than I had intended. I thought leaving it up was better than deleting and reposting 20 hours later, all things considered - my apologies if it turns out someone provides a last-minute resolution on MSE. – RavenclawPrefect Jan 05 '21 at 22:40
  • 4
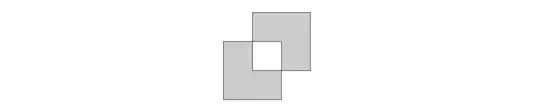
    I asked a different but somewhat related question which was solved by Vytautas Gruslys, Imre Leader, and Ta Sheng Tan. Perhaps they may have some insight into this problem. For example, in their paper they mention that the 6-celled animal XXX.XXX does not tile the plane even though the hole is not completely enclosed. – Timothy Chow Jan 05 '21 at 22:41
  • Yes, I've been making my way through the associated paper (though I haven't finished reading it yet) - perhaps their methods at least yield an upper bound on the necessary dimension to tile a 5-celled animal? (It's not obviously bounded, even knowing that each of them tiles some $\mathbb{Z}^n$.) – RavenclawPrefect Jan 05 '21 at 22:45
  • 1
    Try $2 \times 2$-box plus one cell disconnected from the box. – markvs Jan 06 '21 at 05:12
  • 4
    If the one cell is diagonally adjacent, this tiles the plane (as mentioned in the OP, I have checked all subsets of a $3\times 3$ grid); see here for a computer-generated covering of a $12\times 12$ square which should make clear how the tiling works. Checking several other positions of the additional cell, they all seem to work. – RavenclawPrefect Jan 06 '21 at 06:30
  • 1
    @MarkSapir I think that I can prove that every animal of the form 2x2-box plus disconnected cell tiles the plane (using translations and 180 rotations only). Essentially, my strategy is to show that these animals tile a "jagged strip" whose two boundaries have infinite-dihedral symmetry. – André Henriques May 04 '21 at 22:22

0 Answers0