76

Nearly every mathematician nowadays is familiar with the fact that there is up to isomorphism only one complete ordered field, the real numbers.

Theorem. Any two complete ordered fields are isomorphic.

Proof. $\newcommand\Q{\mathbb{Q}}\newcommand\R{\mathbb{R}}$Let us observe first that every complete ordered field $R$ is Archimedean, which means that there is no number in $R$ that is larger than every finite sum $1+1+\cdots+1$. If there were such a number, then by completeness, there would have to be a least such upper bound $b$ to these sums; but $b-1$ would also be an upper bound, which is a contradiction. So every complete ordered field is Archimedean.

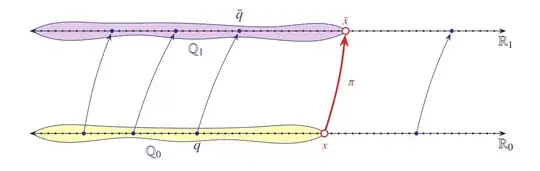
Suppose now that we have two complete ordered fields, $\R_0$ and $\R_1$. We form their respective prime subfields, that is, their copies of the rational numbers $\Q_0$ and $\Q_1$, by computing inside them all the finite quotients $\pm(1+1+\cdots+1)/(1+\cdots+1)$. This fractional representation itself provides an isomorphism of $\Q_0$ with $\Q_1$, indicated below with blue dots and arrows:

categoricity of reals as complete ordered field

Next, by the Archimedean property, every number $x\in\R_0$ is determined by the cut it makes in $\Q_0$, indicated in yellow, and since $\R_1$ is complete, there is a counterpart $\bar x\in\R_1$ filling the corresponding cut in $\Q_1$, indicated in violet. Thus, we have defined a map $\pi:x\mapsto\bar x$ from $\R_0$ to $\R_1$. This map is surjective, since every $y\in\R_1$ determines a cut in $\Q_1$, and by the completeness of $\R_0$, there is an $x\in\R_0$ filling the corresponding cut. Finally, the map $\pi$ is a field isomorphism since it is the continuous extension to $\R_0$ of the isomorphism of $\Q_0$ with $\Q_1$. $\Box$

My expectation is that this theorem is familiar to almost every contemporary mathematician, and I furthermore find this theorem central to contemporary mathematical views on the philosophy of structuralism in mathematics. The view is that we are entitled to refer to the real numbers because we have a categorical characterization of them in the theorem. We needn't point to some canonical structure, like a canonical meter-bar held in some special case deep in Paris, but rather, we can describe the features that make the real numbers what they are: they are a complete ordered field.

Question. Who first proved or even stated this theorem?

It seems that Hilbert would be a natural candidate, and I would welcome evidence in favor of that. It seems however that Hilbert provided axioms for the real field that it was an Archimedean complete ordered field, which is strangely redundant, and it isn't clear to me whether he actually had the categoricity result.

Did Dedekind know it? Or someone else? Please provide evidence; it would be very welcome.

Joel David Hamkins
  • 224,022
  • 1
    This sounds like something Tarski would have known and published (who first proved it). Have you looked at his literature? Gerhard "Society Seems Disordered And Incomplete" Paseman, 2020.06.13. – Gerhard Paseman Jun 13 '20 at 20:21
  • I'm fairly sure Tarski must have known it. But I suspect it must have been known much earlier. – Joel David Hamkins Jun 13 '20 at 20:24
  • See commentary on Twitter at https://twitter.com/JDHamkins/status/1271893175314141185 – Joel David Hamkins Jun 13 '20 at 20:43
  • 14
    This is a great question, but, like all questions about history of science and mathematics, it seems like it should go on HSM. (The standard response is that that site is less active, and at least part of that is because there's so much HSM activity here!) – LSpice Jun 13 '20 at 21:21
  • 19
    @LSpice The standard response is really that the quality of HSM is awful and many experts and interested scholars avoid it as a result. Sending a question there is usually a disservice. – Andrés E. Caicedo Jun 13 '20 at 21:46
  • 16
    @AndrésE.Caicedo, right, but it's circular: HSM will never get any better if the most qualified people keep avoiding it, so those who are interested in HSM should ask and answer questions there, not re-purpose MO for it. We are very strict with new users that MO is only for research-level questions in mathematics; we should be equally strict amongst ourselves. – LSpice Jun 13 '20 at 22:38
  • 7
    @LSpice If a new user wrote such a well-written and clear question, I would strongly support keeping it here on MO. And when I am working with graduate students, I strongly encourage them to look into the history, and read original papers, as part of their research. – Theo Johnson-Freyd Jun 14 '20 at 02:07
  • 19
    @LSpice I think your understanding of what this site is is perhaps too narrow. I feel the question belongs here. – Andrés E. Caicedo Jun 14 '20 at 04:11
  • 1
    @JoelDavidHamkins Hilbert's completeness axiom is not the least upper bound axiom, it is not redundant. Hilbert chose his version of the completeness axiom to be independent of Archimedes axiom. – Julien Narboux Jun 14 '20 at 05:24
  • 1
    @JoelDavidHamkins see [Gio13] Eduardo Giovannini. Completitud y continuidad en Fundamentos de la Geometría de Hilbert : acerca del Vollständigkeitsaxiom. THEORIA. An International Journal for Theory, History and Foundations of Science, 28(1) :139–163, 2013. – Julien Narboux Jun 14 '20 at 05:44
  • 32
    @LSpice One can turn your argument around: it is precisely the excessive efforts to limit interesting questions on MO that has led in recent years to a reduced level of quality and engagement with MO. Have you observed this? To the extent that you are successful in transferring mathematically interesting questions to another site, I would argue that you are working towards the decline of MO. Let's have the interesting questions here! My MO policy has always been: questions are welcome on MO if they are of interest to research-level mathematicians. – Joel David Hamkins Jun 14 '20 at 18:20
  • 2
    @JoelDavidHamkins, I have not noticed any diminution of quality, and I don't know how to measure anyone's engagement but my own. This is one area where SEDE can say for sure, but I suspect that, for a lot of users, the idea of the reduced level of quality and engagement is rather like https://imgs.xkcd.com/comics/the_pace_of_modern_life.png . (I want to say again that this is nothing against your question! I don't want to kill MO; I want HSM to thrive.) – LSpice Jun 14 '20 at 19:12
  • 1
    @JoelDavidHamkins It's also hard for me to tell if there's really been diminution of quality, but if you see a question that you feel has been wrongly closed/deleted, please consider making an appeal at https://meta.mathoverflow.net/questions/223/requests-for-reopen-and-undelete-votes-for-on-hold-closed-and-deleted-question With the scope of your influence at this site, I'd bet this could help bend back MO in a direction you'd prefer. – Todd Trimble Jun 16 '20 at 03:05
  • @Julien Narboux Hilbert's completeness axiom is "R is maximal Archimedean ordered field" ("R is maximal ordered field" characterizes Conway's No) – Zvonimir Sikic Aug 14 '23 at 12:22
  • My of-the-duff guess would have been Landau's Grundlagen. But I looked it up, its date is 1930, so the existing answers below show that I was wrong. – Gerald Edgar Aug 27 '23 at 18:09

4 Answers4

46

Joel, I believe this was first explicitly stated and proved by E.V. Huntington in his classic paper: Complete sets of postulates for the theory of real quantities, Trans. Am. Math. Soc. vol. 4, No. 3 (1903), pp. 358-370. See Theorem II', p. 368.

Edit (June 14, 2020): It is perhaps worth adding that in 1904, the year following the publication of Huntington's paper, O. Veblen published his paper A System of Axioms for Geometry, Trans. Am. Math. Soc. vol. 5, no. 3, pp. 343-384, in which he introduced the idea of a categorical system of axioms. He illustrated his conception with Huntington's above mentioned characterization of the reals (pp. 347-348). No doubt, this is mentioned in the paper referred to below by Ali Enayat.

EDIT (8/27/23)

In light of the doubts raised by Zvonimir Sikic regarding Huntington being the originator of the idea of a categorical system of axioms, it should be noted that while Huntington was well aware that there existed categorical axiom sets in the literature prior to his isolation of the concept, including those axiom sets mentioned by Sikic, he held the view that the earlier writers neither isolated the idea nor expressed any interest in it. He made this point explicitly as follows in 1913 when he provided a novel categorical characterization of Euclidean geometry.

More important than the question of independence is the proof of the sufficiency of the postulates to determine a unique type of system; or, to use a phrase of Veblen’s, the proof that the postulates form a categorical set. Little attention seems to have been paid to this question except by the present writer in connection with the foundations of analysis, and by Veblen in connection with the foundations of geometry; and yet there appears to be no other way of proving that all the propositions of a science are deducible from a given set of postulates, than by showing that the postulates form a ‘sufficient' or ‘categorical' set.” (pp. 524-525)

—Huntington, E. V. 1913. “A Set of Postulates for Abstract Geometry, Expressed in Terms of the Simple Relation of Inclusion.” Mathematische Annalen 73 (4):522–59. (pdf from archive.org)

For what it's worth, David Hilbert was the managing editor of Mathematische Annalen at the time of the publication of Huntington's paper.

Edit: 8/28/23

I should have mentioned in my previous edit, that contrary to Zvonimir Sikic contention, Huntington's paper of 1903 does indeed contain an axiomatization of the ordered field of real numbers as well as a proof of it categorical nature. In Section 2 he provides an axiomatization of the ordered field of real numbers (consisting of 14 axioms including the Dedekind Completeness axiom) and in Theorem II' on page 368 he proves that the axiomatization is categorical.

David Roberts
  • 33,851
Philip Ehrlich
  • 5,915
  • 5
    Huntington's work was based on previous work by Dedekind and Hilbert, but nevertheless, the following article corroborates Ehrlich's claim that E.V. Huntington can be credited to be the first to have formulated and proved the categoricity of the second order theory of the real field (in modern parlance). Completeness and Categoricity. Part I: Nineteenth-century Axiomatics to Twentieth-century Metalogic, by S. Awodey & E. H. Reck (a preprint can be found via http://www.andrew.cmu.edu/user/awodey/preprints/cc/ccI.pdf). It appeared in print in History and Philosophy of Logic, 23: 1–30 (2002). – Ali Enayat Jun 14 '20 at 17:02
  • What about Hoelder's paper from 1901: 'Der Quantitat und die Lehre yom Mass', in Berichte uber die Verhandlungen der Koniglich Siichsuschen Gesellschaft der Wissenschaften zu Leipzig, Matematisch-Physische Classe, 1-64. – Zvonimir Sikic Jun 17 '20 at 11:59
  • It is proved there that Archemedean systems of magnitudes with no minimal magnitudes, are isomorphicaly and densely embeddable in R+ (if they have minima they are isomorphic to Z+). If a system of magnitudes is continuous, i.e. does not have empty Dedekind cuts, then it is isomorphic to R+. Systems of magnitudes is a linearly ordered semigroup with restricted difference. – Zvonimir Sikic Jun 17 '20 at 12:06
  • @philipehrlich Thanks a lot. I completely agree that neither Hilbert nor Holder are originators of the idea of a categorical system of axioms (I suppose it was Veblen). But was that the question? Let me give another example. Who is the originator of the categoricity of the axiomatization of N? I would say Dedekind, although he didn't have the idea of a categorical system of axioms and did not even axiomatize N. – Zvonimir Sikic Aug 28 '23 at 16:12
  • @Zvonimir Sikic. Yes, I suspect Dedekind would get credit with respect to N. See, however, my recent comment regarding your claim about Huntington in your answer to Joe's question. – Philip Ehrlich Aug 28 '23 at 17:47
3

Hilbert's „Über den Zahlbegriff” published in 1900. is the first modern axiomatization of Archimedean fields. To axiomatize R, Hilbert added the maximality axiom (i.e. R is a maximal Archimedean field). He asserted that the existence of the model of the axioms is „nur einer geeigneten Modification bekkanter Schlussmethoden” i.e. „is just a suitable modification of known methods of reasoning”, and uniqueness trivially follows from maximality.

I guess that „bekkanter Schlussmethoden” were the following: If S is an ordered field it contains an isomorphic copy of Q, so let’s call it Q. Every point in S determines a cut in Q. If S is also Archimedean then every cut in Q determines none or one point in S. If S is also maximal then every cut in Q must determine one point in S. Namely, if it doesn’t it could be extended to an Archimedean field with this property, which is by Dedekind construction isomorphic to R. Hence, there is, up to isomorphism, exactly one maximal Archimedean ordered field which is isomorphic to R and every other is, up to isomorphism, contained in R.

This kind of argument has been well known since the time of Dedekind's „Stetigkeit und irrationale Zahlen", i.e. for more than 30 years. Everyone interested in the topic knew the argument, so Hilbert did not consider it necessary to repeat it. This is why I believe that Hilbert proved that maximality uniquely determines R just by stating that the proof is "a suitable modification of known methods of reasoning" (even though he didn't actually formulate the result in terms of isomorphism and didn't give the proof himself).

Hölder published a more general results in „Die Axiome der Quantität und die Lehre vom Mass” from 1901. He proved, in modern terms, that every continous system of magnitudes is isomorphic to R (it is a trivial corollary that every complete ordered field is isomorphic to R). A continous system of magnitudes was axiomatized with trichotomy, associativity, density, positivity (a < a + b), difference (if a < b then there is c such that a+c= b), and Dedekind's axiom (there is no gaps). In his terminology „there is a [real] measure-number for each given magnitude and there is a magnitude for each given [real] measure-number“ and the correspondence preserves the defining properties. It follows taht „if one has two systems of magnitudes, both fulfilling axioms I to VII, then the systems can be explicitly related to each other such that the sums [and order] of corresponding magnitudes also correspond“.

Huntington, in his „A complete set of postulates for the theory of absolute continuous magnitude“ from 1902, wrote: “The set of postulates adopted in the present paper is nearly the same as the second set of Hölder’s, with the exception that Dedekind's postulate of continuity is here replaced by Weierstrass's”. So, Huntington is not concerned with Archimedean fields but with Hölder's systems of magnitudes. He proved in „Complete Sets of Postulates for the Theory of Real Quantities“ from 1903. that „any two assemblages, M (<, +) and M ' (<, +), which satisfy the [Hölder's] postulates 1-10 are equivalent; that is, they can be brought into one-to-one correspondence in such a way that when a and b in M correspond to a' and b' in M', we shall have, a' < b' whenever a < b and a + b will correspond to a' + b' “.

So, Huntington proved the categoricity of (R, <, +) in Section 1 of his 1903 paper, as Hölder did in #15 of his 1901 paper. As Philip Ehrlich pointed out, Huntington also proved the categoricity of (R, <, +, x) in section 2 of his 1903 paper, which Hölder apparently did not. So it may seem that Huntington did something more after all. However, in #16 Hölder defined multiplication in (R,<,+) and proved in #17 that it is unique, so there was no need for special treatment of (R, <, +, x).

Hence, as far as categoricity is concerned, there is nothing in Huntington's work that we do not already find in Hölder's. Therefore, it is not surprising that Ebbinghaus et. al. in references to the chapter on real numbers and their axiomatization (in their book "Zahlen") do not mention Huntington, only Hilbert and Hölder.

Zvonimir Sikic
  • 167
  • How does uniqueness follow trivially from maximality, unless one undertakes the Huntington argument? And does Hilbert claim uniqueness up to isomorphism? Does Hölder? To my way of thinking, realizing that this is an important phenomenon is a significant part of the accomplishment. Huntington does this very clearly. – Joel David Hamkins Aug 23 '23 at 17:05
  • In particular, saying that the axioms were already known earlier is not the same as saying that the categoricity result was known and proved earlier. Was the categoricity theorem even stated clearly by anyone before Huntington? – Joel David Hamkins Aug 23 '23 at 17:42
  • Joel, I edited my answer to respond to your comments. I think that Hilbert was aware of the uniqueness of the Archimedean field that satisfies his axioms because he could certainly have considered the argument I offer as his “bekkanter Schlussmethoden” accessible to everyone. – Zvonimir Sikic Aug 24 '23 at 08:24
  • I don't think that Hilbert had a general concept of categoricity (he used the rather vague semantic/syntactic term complete) and it could be that Huntington's concept of sufficiency was a first step towards that. But the idea was well known in special cases (e.g. Dedekind's theorem that every two simply infinite systems are similar), so I think that in the special case of Archimedean fields the priority is Hilbert's. – Zvonimir Sikic Aug 24 '23 at 08:25
  • Thank for the edit. The argument you offer is the same as Huntington's, the same as what I describe in the OP. From a contemporary perspective, to be sure, this is an elementary argument. But I worry that we make a mistake by viewing things this way from a contemporary outlook. The question is who was first to express and prove the categoricity result. You argue in effect that Hilbert could have done so. Probably that is right, since he was a very talented expert individual. But did he actually formulate the result and give a proof? If not, it seems that Huntington is still the right answer. – Joel David Hamkins Aug 24 '23 at 14:51
  • I've edited it once more to make myself clearer and I would like to see Ehrlich's comment. – Zvonimir Sikic Aug 25 '23 at 10:12
  • Joel, I just read your proof for the first time (before I just skimmed over it, thinking ok I know that) and saw that you can delete the first paragraph (the Archimedean derivation) and the text "by the Archimedean property" in the third paragraph. – Zvonimir Sikic Aug 25 '23 at 16:26
  • I don't think so, because the axioms are merely that it is a complete ordered field, so you need to know that it is Archimedean in order to know that every number is determined by the cut it makes in the copy of $\mathbb{Q}$. There are nonarchimedean ordered fields with elements above every rational, and it seems one must argue that we're not in that case, which is what the first paragraph argument does. – Joel David Hamkins Aug 25 '23 at 16:54
  • For example, in order to know that two different points can't have the same cut in $\mathbb{Q}$, one should consider their difference, which would be smaller than any positive rational number, and so by the Archimedean property they must be equal. – Joel David Hamkins Aug 25 '23 at 17:59
  • By the Archimedean property, every number x∈R0 determines a cut in Q0, [don't need Archimedean property for that], and since R1 is complete, there is a counterpart x¯∈R1 filling the corresponding cut in Q1 [completenes of R1 guaranties that a cut in R1 define x¯, not a cut in Q1, you have to prove that]. Thus, we have defined a map π:x↦x¯ from R0 to R1. This map is surjective, since every y∈R1determines a cut in Q1, and by the completeness of R0, there is an x∈R0 filling the corresponding cut [the same problem]. – Zvonimir Sikic Aug 26 '23 at 06:47
  • It is easier to use supremums: Let X and Y be complete ordered fields. They both contain Q (because they are ordered fields). For every x∈X define Qx = {q∈Q: q<x} and y=supQx in Y (y exists because Y is complete). Function y=y(x) is injective because x<x' implies Qx< Qx' which implies y<y'. It is surjective because for every y∈Y, y=y(x) for x=supQy in X (x exists because X is complete). – Zvonimir Sikic Aug 26 '23 at 06:48
  • 1
    For injectivity, you have to know that distinct numbers in $\mathbb{R}_0$ don't determine the same cut in $\mathbb{Q}_0$, and this amounts to Archimedean. Once that is addressed, your argument is fundamentally the same as mine—you simply fold in the proof of Archimedeanness at each step by using completeness. Meanwhile, I find it insightful to point out that completeness implies Archimedean, since this unifies our understanding of the field, so it is pedagogically better to establish that it is Archimedean. Especially so since Hilbert's axioms include Archimedean and Huntington's do not. – Joel David Hamkins Aug 26 '23 at 10:26
  • In any case, since it is true that completeness implies Archimedean, there seems to be no mathematical reason to object to the observation. One wouldn't be weakening an assumption or somehow making a stronger result by avoiding this observation. – Joel David Hamkins Aug 26 '23 at 10:57
  • Yes, you are right, but it is easy to fold in the injectivity, because there is no q between x and y iff y - x < 1/n for every n iff {1/n} has no infimum. But ( I repeat) to define x¯ you should know that cuts in Q1 defines it. In the Archimedean field X, cuts in Q do the same as cuts in X, but it has to be proved. My point is that using completenes you can bypass this proof. Of course, I agree that completeness=Archimedean+Cauchy is "insightful and unifies" but you introduced Archimedean as a guarantee that "every number x∈R0 determines a cut in Q0" which is true in every ordered field. – Zvonimir Sikic Aug 27 '23 at 12:55
  • Yes, you are right. I have edited my post to say "is determined by the cut it makes", which is what I had meant. – Joel David Hamkins Aug 27 '23 at 13:20
  • @Zvonimir Sikic. Your claim about Huntington's paper of 1903 is mistaken. In Section 2 he provides an axiomatization of the ordered field of real numbers (consisting of 14 axioms including the Dedekind Completeness axiom) and in Theorem II' on page 368 he proves that the axiomatization is categorical. – Philip Ehrlich Aug 28 '23 at 17:44
  • @Philip Ehrlich, Yes you are right, I ignored section 2. But there is a reason for that which I explain in my edited answer. – Zvonimir Sikic Aug 29 '23 at 07:28
  • @Zvonimir Sikic. Your point about Hölder proving the uniqueness of multiplication (assuming the left and right distributive laws) is a good one. So, while, Hölder may not have proved categoricity, what he proved certainly naturally suggests it. – Philip Ehrlich Aug 29 '23 at 21:31
3

The key question here is that Dedekind complete implies Archimedean, as in the first paragraph of Joel's Proof.

This was shown by Otto Stolz, in Zur Geometrie der Alten, insbesondere über ein Axiom des Archimedes, Mathematische Annalen, 22(4):504–519, 1883.

Apparently Stolz was persuaded to retract this paper.

I confess that I can't read German with any fluency and only got through the first part of the paper, but it does seem to me that that contains the correct argument that Joel states. Therefore Stolz deserves the credit.

The later part of the paper looks rather strange, but that's in part because I didn't follow the text.

However, Mikhail knows more about the history and will no doubt explain.

Footnote: I conjecture that a version of Conway's "surreal" numbers using computably enumerable subsets instead of general ones might be able to avoid Stolz's argument and yield a Dedekind complete but non-Archimedean field.

Some years ago, I put this conjecture to (the late) John Conway, he scratched his head and said "maybe".

Paul Taylor
  • 7,996
  • 3
    This is very interesting, if it is true that Stolz has a clear statement of the categoricity result, since it is much earlier than Huntington. Can we have any German readers translate the relevant parts? To my way of thinking, however, the categoricity result goes strictly beyond merely observing that completeness implies Archimedean. That is key, of course, but categoricity is an important further idea of its own, of central importance and naturally in contemporary thought. It is precisely the question—when did this change occur? Huntington has essentially the contemporary view. – Joel David Hamkins Aug 27 '23 at 19:45
  • Or are you claiming only that Stolz has the complete$\to$Archimedean result only? If so, then this seems insufficient for credit for the categoricity result. – Joel David Hamkins Aug 27 '23 at 19:55
  • @JoelDavidHamkins: As a categorist, I'm not keen on the (model-theoretic) notion of "categoricity". After the complete/Archimedean question, I don't see the difficulty. (There are constructivity issues, on which my view is here, but you asked the question classically.) – Paul Taylor Aug 27 '23 at 20:18
  • 1
    Stolz is one of my favorite historical figures and I have extensively read and written about his work (e.g. https://www.researchgate.net/publication/225675816_The_Rise_of_non-Archimedean_Mathematics_and_the_Roots_of_a_Misconception_I_The_Emergence_of_non-Archimedean_Systems_of_Magnitudes). The claim that he had a notion of categoricity strike me as far fetched. He also never wrote about ordered fields. He worked primarily on the positive cones of ordered abelian groups, and in 1891 succeeded in proving that the positive cone of a Dedekind complete ordered abelian group is Archimedean,... – Philip Ehrlich Aug 27 '23 at 21:11
  • (continued), his earlier attempts having beed criticized by others including Veronese. This is all discussed in the paper referred to above. – Philip Ehrlich Aug 27 '23 at 21:15
  • 3
    @PaulTaylor To my way of thinking, the categoricity results of Dedekind and Huntington and so forth are the origin of the philosophy of structuralism in mathematics, because they enable us to refer to our familiar mathematical structures by identifying the features that characterize those structures up to isomorphism. I would think this is as important in category-theoretic foundations as in any other, whether set theory or type theory or what have you. So I was surprised to hear that you disparage the categoricity results (which are not theorems of model theory but mathematics generally). – Joel David Hamkins Aug 27 '23 at 21:54
-3

I am confused by the failure to recognize the set-theoretic issue. Without requiring Archimedeanity, Conway’s Surreals are ordered, and satisfy the field axioms, and have no gaps! The only reason they can’t be a complete ordered field, if you use a no-gap definition of “completeness” rather than one involving sequences or the Archimedean property or a least upper bound property, is that they are too big to be a set.

You need to give a simple answer to “why aren’t the surreal numbers a second complete ordered field?”

Joe Shipman
  • 819
  • If we were to use a surreals-style "no-gap" account of completeness, then the real field $\mathbb{R}$ itself would fail to be complete, since it has an unfilled gap between $0$ and the positive elements. To be sure, the surreal field is based on the idea of iteratively filling all such gaps, but no set-sized structure can be complete in that no-gaps sense. This is why, when speaking of the complete ordered field, we use the LUB account of completeness, which the surreal numbers lack. For example, there is no LUB in the surreal numbers to the infinitesimal surreal numbers. – Joel David Hamkins Aug 28 '23 at 15:26
  • Joe, Conway’s No is non-Archimedean ordered field which has Dedekind's gaps. Perhaps, your point is that it satisfies Cantor's axiom? Because it does. If you worry that No is a real class, you may limit it to the ordered field of surreal numbers built up to the "moment" ε0 and it is still non-Archimedean ordered field which has Dedekind's gaps, but satisfies Cantor's axiom. Let's add that No is to ordered fields what R is to Archimedean ordered fields. Just as every Archimedean ordered field is contained in R, so every ordered field is contained in No. – Zvonimir Sikic Aug 28 '23 at 15:34
  • Yes, there are "gaps" in Conway's number system. They are discussed on pages 37--38 of On Numbers and Games. – Paul Taylor Aug 28 '23 at 19:43
  • They’re not really “gaps” that are legal in ZFC! That’s my point. Any “gap” that can be defined by giving two sets of Numbers L and R such that every element of L is < every element of R is already filled by a surreal number. You can only make a true “gap” by using left and right “classes”, not sets! – Joe Shipman Aug 28 '23 at 21:16
  • 1
    What in the world does "legal in ZFC" mean? You make ZFC sound like a police state! The fact is that $\mathbb{R}$ has no gaps at all (neither "legal" nor "illegal")! – François G. Dorais Aug 29 '23 at 09:03
  • @FrançoisG.Dorais $\mathbb{R}$ does have unfilled gaps, everywhere, in the sense that Joe is using, since one can find two disjoint sets $L$, $R$ with every element of $L$ strictly below every element of $R$, but no element $x\in\mathbb{R}$ having $L<x<R$. Take $L=(-\infty,0]$ and $R=(0,\infty)$. The legality question is just whether $L$ and $R$ are sets or proper classes. In the surreals, all gaps defined by sets this way are inhabited by the surreal number ${L\mid R}$, which was created specifically to occupy this gap. But there are unfilled surreal gaps specified by proper classes. – Joel David Hamkins Aug 29 '23 at 11:09
  • If we consider dense linearly ordered sets, without requiring addition or multiplication properties, but still require the LUB property (in the form “if Y is a nonempty subset of X such that there exists x in X with y<=x for all y in Y, then there is a least such x”), what possibilities arise that are not simply intervals of reals? I can think of a few…. – Joe Shipman Aug 29 '23 at 14:08