13

Which convex bodies can be captured in a knot?

This question is based on the discussion in "Is it possible to capture a sphere in a knot?". We assume that the knot is made from unstretchable, infinitely thin rope.

Comments:

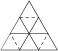
  • By the construction Anton Geraschenko, the question is equivalent to existence of a graph embedded in the surface of the convex body that locally minimize the total length. Such embedding exists on some convex bodies, for example on an equilateral triangle shown on the diagram (and on anything sufficiently close).

three loops on triangle that locally minimize the total length

  • According to the original question a ball cannot be captured (in fact it cannot be captured in a link with 3 components). Moreover a circular disk cannot be captured see my answer (thanks to Wlodek Kuperberg for asking). Likely the same idea works for all convex bodies of revolution. Maybe all convex bodies of general position can be captured.
RobPratt
  • 5,169
Anton Petrunin
  • 43,739
  • 1
    Can a circular disk be captured? Does it make a difference whether we use a knot or an unknot? – Wlodek Kuperberg Jun 02 '20 at 00:38
  • 1
    Thanks. Is there any convex body that can be captured by an unknot? The diagram with the equilateral triangle is unclear: knot? not? – Wlodek Kuperberg Jun 02 '20 at 03:06
  • @WlodekKuperberg about unknot, an unknot can be tangled at the intersection point; so that the same argument shows that it cannot be removed. But if you allow the thread to go thru it self, then no --- it cannot be captured --- the equidistant move reduces the length. – Anton Petrunin Jun 23 '20 at 19:37
  • The regular tetrahedron and the cube seem like a natural pair of test cases (both can be nicely unrolled onto the plane, as long as you avoid the vertices). – zeb Jun 23 '20 at 19:52
  • @zeb yes, it seems that one can modify the example for triangle to show that tetrahedron can be captured. Most likely any convex polyhedron can be captured, but that will require a new idea. – Anton Petrunin Jun 23 '20 at 22:57

1 Answers1

2

A circular disc cannot be captured. Likely the same idea can be used to show that any convex body of revolution cannot be captured.

It can be proved using a small variation of the idea as in the original answer. It is sufficient to show that infinitesimal Möbius tranform $m$ of the disc can shorten the wrapping length while preserving the crossing pattern. Once it is proved, moving in this direction will eventually allow the disc to escape.

Choose a Möbius tranform $m$ of the unit disc that is close to the identity map. Denote by $u$ its conformal factor. Denote by $U(r)$ the average value of $u(x)$ for $|x|=r$. It is sufficient to show that $U(r)\le 1$ and the inequality is strict for $r<1$. In this case by rotating the knot and applying the Möbius tranform will shorten the length.

Consider the circle $C_r$ of radius $r$ centered at the origin. Denote by $r'$ the radius of $m(C_r)$. Observe that $U(r)=r'/r$. Evidently $r'\le r$ if $r\le 1$ and $r'< r$ if $r< 1$, whence the result.

Anton Petrunin
  • 43,739