Closed geodesics on constant positive Gauss curvature surfaces

Question

Can we show that geodesics with a rational radius $ r_{mid-equator} =a q/p \,(p>q ) $ at mid-equator on a spindle type surface of revolution of constant Gauss curvature $ (K=1/a^2 \, $in $\, \mathbb R^3 ) $ form closed loops around the symmetery axis in terms of $ (p, q)$? Is the arc length of a loop/orbit expressible as being related to $ (2 \pi a, p,q)?$

If a Riemann sphere radius $a$ is isometrically mapped/deformed without twist (roll squeezed) along equator will its geodesics deform this way due to isometry?

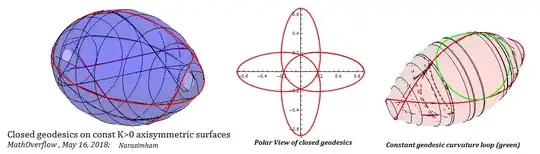
The figure shown below is drawn for $ q=2,p=3 $ respecting geodesy/constant $K$ in the present investigation. In all such cases numerical work established/ confirmed existence of such closed loops.

What existing related literature can be found on the topic?

Thanks in advance of your response.

EDIT1:

At first $k_g=$ for constant geodesic curvature closed loops were expected (by me) but not the entire geodesic line closing in as a single loop line as that would be counter-intuitive. In the picture shown numerical value $a k_g=1.4$ is assumed.

EDIT2:

The following geometrical results of radius and arc length are now verified in this investigation and reported here:

Radius variation with respect to arc length $s$, $ \alpha$ being angle between arc projection and symmetry axis at mid-equator start:

$$ \left(\frac{r}{r_{mid-equator}}\right)^2 + \left(\cos \alpha \cdot \sin \frac{s}{a}\right)^2=1 \tag1 $$

which can be also written $ r_o= r_{cuspidal-equator}$

$$ \cos \dfrac{s}{a} =\sqrt{\dfrac{r^2-r_0^2}{r_1^2-r_0^2}} \tag2 $$

Arc length of a single circuit $ L_{circuit}$ from right cusp equator to right cusp equator back via left cusp equator is found to be:

$$ L_{circuit}= 2 \pi a \tag 3$$

as can be expected in full isometric mappings.

For an image of a "Zoll surface," see this earlier question. Allowing negative curvature leads to different surfaces. — Joseph O'Rourke, May 17 '18 at 00:45
May I observe in this context, if I understood Bill Thruston properly of the earlier question.. 1) If force $F$ along a string is constant then the moment around symmetry axis $F\cdot ( r \sin \psi) $ is constant, $\psi$ is the angle thread makes to meridian. 2) A physical action of winding of string on a cylinder should result in a thick bead / lump at the ends but not at middle of cylinder after several cycles of geodesics are gone through, as mentioned in his reply. ( contd).. — Narasimham, May 28 '18 at 09:49

score 10 · Accepted Answer · answered May 16 '18 at 08:55

10

The answers to your questions about geodesics on such surfaces can be found in A. L. Besse's book Manifolds all of whose geodesics are closed (1978, Springer Ergebnisse series). Especially, you should have a look at Chapter 4 on surfaces. In particular, it is true that all of the geodesics that stay in the smooth part of the surface are closed, and their length is known in terms of $a$, $p$, and $q$.

answered May 16 '18 at 08:55

Robert Bryant

106,220

Thanks for the reference. Sections 4.11, 4.11 theorem, 4.13 Tannery surfaces etc. but Google book review is inturrupted at essential places. BTW, do such closed geodesics have any practical applications? – Narasimham May 17 '18 at 00:39
@Narasimham: I wouldn't go so far as to say "practical," but such a surface can roll on the plane along the geodesic, indefinitely following a straight line. Also such a geodesic partitions the curvature into exactly $2 \pi + 2 \pi$. – Joseph O'Rourke May 17 '18 at 00:48

Closed geodesics on constant positive Gauss curvature surfaces

1 Answers1