7

Given a simple closed curve in the plane, there is a homeomorphism from the unit open disk to the interior of the curve. The homeomorphism can be taken conformal, this is the uniformisation theorem.

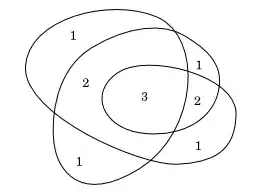
Is there a version of this result for closed curves that are not simple?

For example, given a $C^1$ closed curve $\gamma: S^1 \rightarrow {\bf R}^2$ with finitely many self-intersections, all of them transverse, is there a continuous map (maybe even conformal) from the unit open disk to the plane, such that the number of preimages of any point in ${\bf R}^2\backslash \gamma(S^1)$ is equal to the absolute value of the number of turns the curve makes around the point?

$\hskip 1in$ non simple closed curve

coudy
  • 18,537
  • 5
  • 74
  • 134
  • 1
    What would such a map look like for the figure-8 curve? – Mikhail Katz Jul 06 '17 at 14:03
  • @Katz Twist the disk in three space, project it on a plane. So there is a line dividing the disk that projects exactly on the double point. Perhaps asking for all the number of turns to be of the same sign is a necessary condition for a conformal map. – coudy Jul 06 '17 at 14:11
  • 1
    @coudy: The map you describe in the comment is not conformal, and not even open. Of course there is always a continuous map: a continuous map of a circle extends continuously in the disk. So what are you really asking? – Alexandre Eremenko Jul 06 '17 at 20:49
  • @Eremenko. An arbitrary extension will not necessarily give the expected multiplicity. Read again the question and look at the diagram. – coudy Jul 07 '17 at 06:19
  • @coudy Already in the figure-8 example, you need to count multiplicities with sign. An arbitray extension will give correct multiplicities (counted with sign). Do you want an extension where no preimages cancel because of sign issues? – Sebastian Goette Jul 07 '17 at 07:54
  • 1
    @goette. The question is the following. Given a C1 closed curve γ:S1→R2 with finitely many self-intersections, all of them transverse, is there a continuous map (maybe even conformal) from the unit open disk to the plane, such that the number of preimages of any point in R2∖γ(S1) is equal to the absolute value of the number of turns the curve makes around the point? – coudy Jul 07 '17 at 19:50

1 Answers1

3

It sounds like, to some extent, what you are asking is whether an immersed closed curve in the plane can be extended to an immersion of a disk. This would yield the multiplicities that you seek; however, such an extension is not always possible. Necessary and sufficient conditions were first given in the thesis of Blank in 1967. For instance see this paper for more on this topic and references.

Mohammad Ghomi
  • 7,047
  • 1
    There are some more references at this MO question https://mathoverflow.net/questions/100224/which-immersed-plane-curves-bound-an-immersed-disk – j.c. Oct 13 '17 at 13:47