4

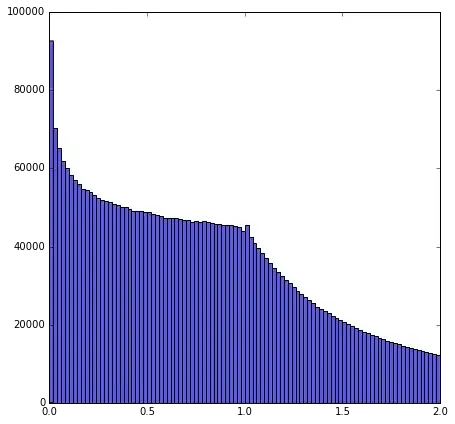
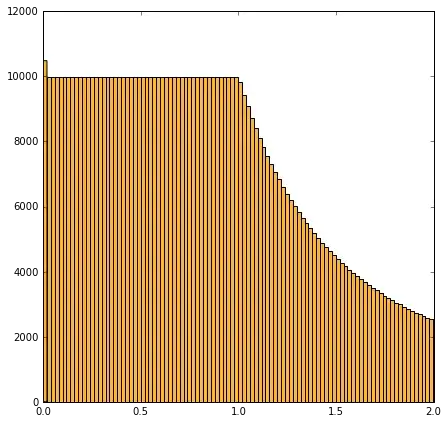
I did some numerical experiments about $\{ \frac{a}{b}: a,b \in A, \;a < \, b\}$ for various integer sets $A$. Does anyone recognize these densities?

Here is $A = \{ p: \text{prime}\}$

enter image description here

Here is $A = \mathbb{Z}$

enter image description here

Here is if $\{ (a,b): a < 2 \, b, \; \gcd(a,b) = 1 \}$. Does this uniform distribution surprise everybody?

enter image description here

Literature on each of these could be interesting. I know there is discussion about the primes case being dense already:

By default I can look for the Weyl Equidistribution Theorem. We are told to evaluate sums:

$$ c_N(m) = \sum_{0 < a < b < N} e^{2\pi i m \frac{a}{b}} $$

These are the sums of Ramanujan, $c_q(n)$. This paper of Huxley states in the affirmative, and - in usual style - the result is so obvious he does not prove it.

In another place Huxley works it out. He shows (unconditionally) just reasoning about fractions:

$$ \sum_{n=1}^N e^{ 2\pi i \, m \frac{a}{b}} \ll d(m) \sqrt{N} $$ and this is Weyl's criterion. The other lemma I like is: Let $0 < x_n < 1$ be the Farey fractions between $0$ and $1$:

$$ \sum_{n=1}^N e(m x_n) = \sum_{d|m} d \left[ M( \tfrac{Q}{d}) \right] $$

where $M(x) = \sum_{m \leq x} \mu(m)$. No effort was taken to optimize exponent. This is already equivalent to $M(x) = o(x)$.

This is taken from Chapter 1 Huxley's book Area, Lattice Points, and Exponential Sums

Community
  • 1
john mangual
  • 22,599

1 Answers1

6

The equidistribution in the last graph is equivalent to the prime number theorem, the optimal speed of equidistribution is equivalent to the Riemann hypothesis. The way you get there is by taking Fourier transform of the empirical measure, and when the smoke clears, the decay of coefficients is equivalent to the fact that $\sum_{n<x} \mu(n) = o(x).$

EDIT A nice exposition can be found in this University of Edinburgh senior project.

Igor Rivin
  • 95,560
  • Are you sure? It looks to me like the simpler fact that $\sum_{n<x} \mu(n)=o(x^2)$. – Will Sawin Aug 14 '16 at 18:34
  • @WillSawin Did you note that $Q \asymp \sqrt{N}$ ? I have that $\sum_{n<x} \mu(n)=O(x)$ which is somewhat less than the PNT. – john mangual Aug 16 '16 at 16:46
  • @johnmangual The equidistribution follows from $\sum_{d|m} d M(Q/d) = o(N)$, which follows from $M(x) = o(x^2)$, because then $M(Q/d)=o(Q^2/d^2)=o(Q^2)=o(N)$. We can assume $m=O(1)$ so $d=O(1)$ and the sum is finite. – Will Sawin Aug 16 '16 at 17:34
  • @WillSawin The book uses $\sum_{n < x}\mu(n) \leq x$ which even I can verify. Unfortunately, this is definitely not the PNT. Even if I use $\zeta(1+it) \neq 0$ I still need the Wiener-Ikehara (or something) to prove $\sum_{n < x} \mu(n) = o(x)$. At least, if I find some way to get better than $N^{1/2}$ on these Weyl averages, it's equivalent to PNT. – john mangual Aug 16 '16 at 18:40
  • @johnmangual Exactly. I am saying that the equidistribution statement follows from the simpler bound $\sum_{n <x} \mu(n) \leq x$ and is thus not equivalent to the PNT. – Will Sawin Aug 16 '16 at 19:35
  • @johnmangual Which book are you referring to? – Igor Rivin Aug 16 '16 at 20:25
  • @WillSawin I am very confused. $|\mu(n)| \leq 1,$ are you being sarcastic about the "simpler fact"? – Igor Rivin Aug 16 '16 at 20:26
  • Huxley's book on Areas and Lattice Points. That's just the first book I found. He shows Farey Fractions are equidistributed in $\mathbb{R}$ (they had better be!) and with error about $\frac{1}{\sqrt{N}}$ and if you do better than that one should get PNT and if one gets $\frac{1}{\sqrt[4]{N}}$ that might be RH. – john mangual Aug 16 '16 at 22:34
  • @johnmangual Ah, OK, thanks! I was not actually aware of any reference... – Igor Rivin Aug 16 '16 at 22:53
  • @johnmangual see also the reference in the edit... – Igor Rivin Aug 16 '16 at 23:01
  • 1
    @IgorRivin I am not being sarcastic, I'm just trying to make a very slight correction but not communicating very clearly. I think your first statement is wrong because the Prime Number Theorem does not follow quickly from the equidistribution statement. The bound that the equidistribution statement is equivalent to is $\sum_{n < x} \mu(n)= o(x^2)$, which is trivial because, as you note, $|\mu(n)| \leq 1$. I agree that optimal equidistribution is equivalent to the Riemann hypothesis. – Will Sawin Aug 17 '16 at 00:02