Define a rational $d$-simplex as a simplex in $\mathbb{R}^d$ such that the measure of all its $k$-dimensional faces, $k \ge 1$, is rational. So a rational triangle has rational edge lengths and rational area. A rational tetrahedron has six rational edge lengths, four rational face areas, and rational volume. And so on. (By scaling these could all be natural numbers.)
Q. For which $d$ is it known that there are an infinite number of non-similar rational simplices in $\mathbb{R}^d$ ?
(The non-similar restriction is to exclude scalings.) This is in some sense a request to update Richard Guy's Unsolved Problems In Number Theory, Problem D22. But I am specifically interested in the boundary between an infinite number of examples, and a finite class of distinct examples. Is that boundary: Yes ($\infty$) for $d \le 3$, and No (or unknown?) for $d > 3$? Or is the boundary: $d \le 2$ vs. $d > 2$? Or some other divison?
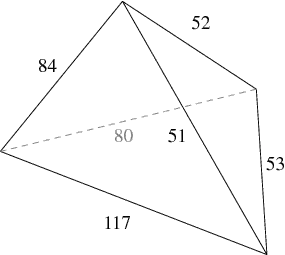
(Image from MathWorld. Face areas $1170, 1800, 1890, 2016$; volume $18144$.)
Update. Answered in the comments by j.c. and Moritz Firsching: Infinite families are known up to $d=3$, but not for $d \ge 4$ (and it seems unlikely even in $d=4$).