4

Let $a$ and $b$ be two points in the plane. Let's choose a point $c$ uniformly from the circle of radius $r$ with $a$ as center and choose a point $d$ uniformly from the circle of radius $r$ with $b$ as the centre of this circle. Let $X$ be the eucleadian distance between $c$ and $d$. What's the density function of $X$? Is it hard compute? P.S. I know how to do it when $a=b$.

Mudi
  • 93
  • MO is for math research questions. Is there a research angle to this question? – Gerry Myerson Nov 11 '15 at 12:05
  • Yes Gerry, I want to compute average degree of nodes placed, roughly, in a grid where adjacency defined in terms of distance. Problem arises in sensor networks. – Mudi Nov 11 '15 at 14:19
  • 1
    Do you mean the points are drawn from the interiors or from the boundaries? – Douglas Zare Nov 11 '15 at 15:48
  • 1
    What do you get when $a=b?$ – Igor Rivin Nov 11 '15 at 16:39
  • Yes, I am sorry I meant to choose uniformly from the interior of circle.

    When $a=b$, the expression doesn’t look pretty (not to me at least) but the argument/procedure is simple enough (It’s described in Tuckwell’s Applications of Probability Theory). Anyway here it is. $f_X(x) = \frac{2x}{\pi r^2}( 2 \arccos(\frac{x}{2r}) - \frac{x}{r} \sqrt{ 1-{(\frac{x}{2r}) }^2} )$.

     – Mudi Nov 11 '15 at 17:17

1 Answers1

2

Empirically, the distribution appears approximately normal. Below is the distribution for $10^6$ pairs of $c,d$-points, $r=1$, $\| a - b \|=3$ (so the closet $X=\| c - d \|$ distance possible is $1$, and the furthest distance possible is $5$.

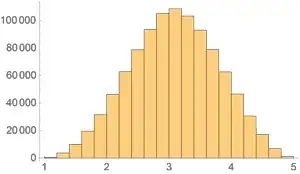
          DistanceDistribution
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • Seeing @DouglasZare's question, I assumed that "from the circle" and "in unit circles" mean from the interior of the circles (rather than on the circle boundaries). – Joseph O'Rourke Nov 11 '15 at 16:29
  • This is interesting - it didn't occur to me to check it empirically. Can you think of a way to prove this hypothesis? Thanks. – Mudi Nov 11 '15 at 17:32