Mysterious identity between numbers of odd/even meander systems

Question

Definitions:

An upper arch system of order $n$ is a subset of the plane consisting of $n$ non-intersecting closed semicircles in the upper half-plane whose endpoints belong to the set $\{(k,0)\mid 1\leqslant k\leqslant2n\}$.

It is well known that the number of all upper arch systems of order $n$ is $C_n=\frac{(2n)!}{n!(n+1)!}$, the $n$th Catalan number.

Lower arch systems are exactly the same thing in the lower half-plane.

A (closed) meander system of order $n$ is a union of an upper and a lower arch system of order $n$.

Let $MS_n$ be the number of all meander systems of order $n$. Thus $MS_n=C_n^2$.

Call a meander system odd, resp. even, if it has odd, resp. even number of connected components.

Illustrations:

(The first is an even meander system of order 6, the second - an odd meander system of order 8.)

Let $OMS_n$, resp $EMS_n$ be the number of odd, resp. even meander systems of order $n$.

Numerical evidence suggests that for all $k$ one has

$$OMS_{2k}=EMS_{2k},$$ $$OMS_{2k+1}=EMS_{2k+1}+MS_k.$$

Does anybody know whether this is true?

(Remark: if it is true, then obviously $OMS_{2k}=EMS_{2k}=\frac12C_{2k}^2$ and $OMS_{2k+1}=\frac12\left(C_{2k+1}^2+C_k^2\right)$, $EMS_{2k+1}=\frac12\left(C_{2k+1}^2-C_k^2\right)$)

Final remark: as kidly pointed out by Gjergji Zaimi in a comment below, this is in Meander, Folding and Arch Statistics by Di Francesco, Golinelli and Guiller (6.16, page 51). So I have to apologize for forcing you guys to think on the question answered 20 years ago.

Still it was fun, wasn't it?

Answer 1

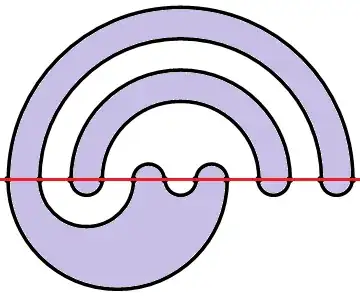
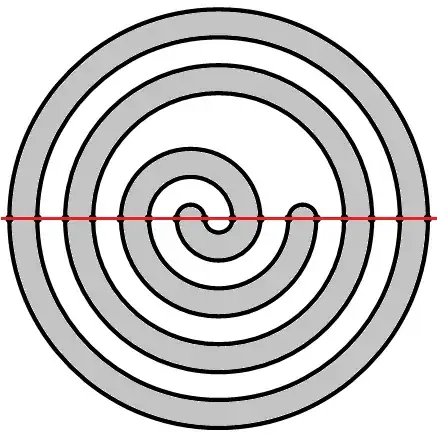
Let me get the skeleton of an answer down here and then I can edit in more details if you want later.

An arch system can be represented as a set of ordered pairs; for example, in the first example the upper arch system is $$\{(1,12),(2,11),(3,10),(4,9),(5,6),(7,8)\}$$ and the lower arch system is $$\{(1,8),(2,5),(3,4),(6,7),(9,10),(11,12)\}.$$ The numbers in each pair are always of opposite parity.

Define the parity of an arch system as $$ \prod_{\text{pairs }(a,b)}(-1)^{\frac{b-a-1}{2}} $$ so the parity of the upper arch system is $-1$ and the parity of the lower arch system is $+1$.

It is not hard to see that the parity of a meander $m$ (where odd is identified with $-1$ and even with $+1$) is equal to the product of the parities of its constituent arch systems and $(-1)^{\text{order}(m)}.$

EDIT:

Consider a meander where the upper arch system contains two pairs of the form $(a, b)$ and $(a+1,a+2)$. Compare this to the meander where we replace these two arches with $(a,a+1)$ and $(b,a+2)$. It is evident that this swaps the parity of the meander and of the arch system. Any arch system can be reduced to $\{(1,2),\ldots,(2n-1,2n)\}$ by a finite number of these moves.

(end edit)

Next, let's count odd and even arch systems. Let $A_{-1}(n)$ and $A_{+1}(n)$ be the number of $-1$ and $+1$ parity arch systems respectively (formally set $A_{+1}(0)=1$ and $A_{-1}(0)=0$). Then by looking at whatever is paired with $1$ we get the recursions \begin{align*} A_{-1}(n)&=\sum_{i=0,2,\ldots} \big(A_{-1}(i)A_{+1}(n-i-1) + A_{+1}(i)A_{-1}(n-i-1)\big)\\ &+\sum_{i=1,3,\ldots}\big(A_{-1}(i)A_{-1}(n-i-1) + A_{+1}(i)A_{+1}(n-i-1)\big) \end{align*} and \begin{align*} A_{+1}(n)&=\sum_{i=1,3,\ldots} \big(A_{-1}(i)A_{+1}(n-i-1) + A_{+1}(i)A_{-1}(n-i-1)\big)\\ &+\sum_{i=0,2,\ldots}\big(A_{-1}(i)A_{-1}(n-i-1) + A_{+1}(i)A_{+1}(n-i-1)\big) \end{align*}

Simple rearrangement of the sums shows that $A_{+1}(2k)=A_{-1}(2k)$, which implies that both are $\frac{C_{2k}}{2}$.

EDIT: inductive argument added.

The following inductive argument shows that $A_{\pm 1}(2k+1)=\frac{C_{2k+1}\pm(-1)^k C_k}{2}$.

If $n\equiv1\pmod 4$ then when $i$ is odd, then one of $\{i,n-i-1\}$ is $1\pmod 4$ and one is $3\pmod 4$.

By induction, the sum above, for $A_{-1}(n)$, say, is: \begin{align*} A_{-1}(n)&= \sum_{i=0,2,\ldots} \frac{C_iC_{n-i-1}}{2}\\ &+\sum_{i=1,3,\ldots}\frac{1}{4}\left( \left(C_i+C_{\frac{i-1}{2}}\right)\left(C_{n-i-1} - C_{\frac{n-i-2}{2}}\right) + \left(C_i-C_{\frac{i-1}{2}}\right)\left(C_{n-i-1} + C_{\frac{n-i-2}{2}}\right)\right) \\ &=\sum_{i=0,1,2,\ldots} \frac{C_iC_{n-i-1}}{2} -\sum_{i=1,3,\ldots} \frac{C_{\frac{i-1}{2}}C_{\frac{n-i-2}{2}}}{2} \\ &=\frac{C_n}{2} -\sum_{j=0,1,2,\ldots}\frac{C_{j}C_{\frac{n-1}{2}-j-1}}{2} =\frac{C_n}{2} - \frac{C_{\frac{n-1}{2}}}{2}. \end{align*} The other cases of the induction (for $n\equiv 3\pmod 4$ and/or if one wants an independent induction for $A_{+1}(n)$ are similar.

(end edit)

Then using the relationship between parity of meanders and parity of arch systems the result follows by arithmetic.

I can supply more details about the recursion, the rearrangement, the inductive argument, or the final arithmetic once the $A_{\pm 1}$ have been determined, if desired.

Answer 2

It is not a solution, just additional observation. It is better to devide Catalan numbers into two parts $$C_n=O_n+E_n,$$ where $O_n$ ($E_n$) is the number of "odd" ("even") upper arch systems of order $n$: the number with odd (even) river regions where "river region" are regions from upper half-plane which will be inside connected components of future meander. (On the first diagram we have 4 river regions in the upper half-plane and 4 river region in the lower half-plane. On the second diagram 5 and 4) These sequences are known as http://oeis.org/A007595 and http://oeis.org/A000150.

Then $$OMS_{k}=2E_k\cdot O_k,\qquad EMS_{k}=O_k^2+E_k^2.$$

On this way it is necessary to prove that parity of meander is a sum of parities of upper and lower arch systems.

EDT: It was done in the answer of Gabriel C. Drummond-Cole. Also from his answer follows that
$$(-1)^{\text{parity of river regions}}=\prod_{{\rm pairs}(a,b)}(-1)^{\frac{b-a+1}2}.$$

(Images added by OP - he thought it would be more instructive this way. Parity of an arch system is parity of the number of connected components of the gray subset of the corresponding half-plane. Note that one may do the coloring of one half without knowing anything about the other.)