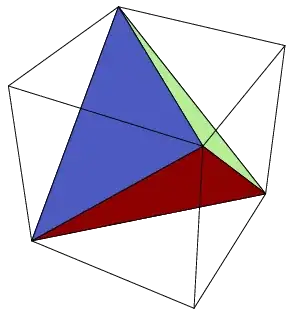
Allow me look at one aspect, or special case, of your question, namely "finding the largest regular 3-dimensional tetrahedron inscribed in a d-dimensional unit cube".
I. $4$-cube
I can find the following largest regular $3$-simplex inscribed in a 4-cube. Essentially I used the same methods as described in the paper Computing Maximal Copies of Polyhedra Contained in a Polyhedron, Experimental Mathematics Vol. 24 (2015), Issue 1, pp.98-105 or in this MathOverflow answer: On maximal regular polyhedra inscribed in a regular polyhedron.
First I solve a quadratically-constrained non-linear program, then I use Newton's method to find high precision solutions, convert them to algebraic solutions using integer relations, and finally check the solutions using calculations in extensions of $\mathbb{Q}$.
Since the tetrahedron is 3-dimensional, we can visualize the configuration by taking the intersection of the affine span of the tetrahedron with the cube. This gives combinatorially a prism over a hexagon and looks like this:
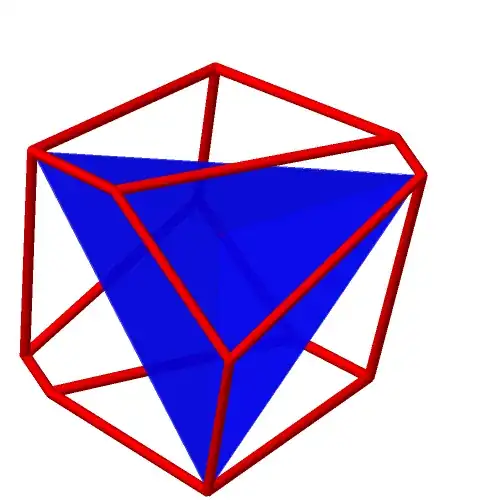
Click here for an animation
If the $4$-cube is given as $[0, 1]^4$, then the coordinates of the tetrahedron are
$$ (a, 0, 0, 1) \\
(b, 1, 0, 0) \\
(0, c, 1, 0) \\
(1, d, 1, e)
$$
where $a,b,c,d$ and $e$ are some algebraic numbers of degree 8. in fact, we have
$$\begin{align}
a &= \text{ zero near }0.2417346828\text{ of }\\ &128x^8 - 128x^7 + 464x^6 - 296x^5 + 959x^4 - 1568x^3 + 958x^2 - 248x + 23\\
b &= \text{ zero near }0.5021530192\text{ of }\\ &128x^8 - 384x^7 + 208x^6 + 328x^5 - 361x^4 - 16x^3 + 170x^2 - 56x - 1\\
c &= \text{ zero near }0.09686099894\text{ of }\\ &128x^8 - 768x^7 + 2224x^6 - 3848x^5 + 4119x^4 - 2452x^3 + 542x^2 + 60x - 9\\
d &= \text{ zero near }0.6856472601\text{ of }\\ &512x^8 - 3072x^7 + 9408x^6 - 17632x^5 + 19388x^4 - 10480x^3 + 500x^2 + 2000x - 625\\
e &= \text{ zero near }0.8492045976\text{ of }\\ &8x^8 - 16x^7 + 16x^6 - 16x^5 + 6x^4 - 4x^3 + 6x^2 - 1\\
&\text{and also,}\\
f &= \text{ zero near }1.4379908587\text{ of}\\ &8x^8 - 16x^7 - 28x^6 + 68x^5 - x^4 - 48x^3 + 24x^2 - 16\\
\end{align}.$$
where $f$ is the edge length of this regular tetrahedron.
From the case $(3,4)$, we can observe the following:
In an optimal solution, there might not be a vertex of the simplex coincident with a vertex of the cube (as one might expect from examining the cases $(2,2)$ and $(3,3)$)
For the $(3,4)$ configuration, three vertices of the tetrahedron lie on edges of the cube and one on a 2-face.
As you guessed the solution is at least somewhat "not simple": All coordinates of the optimal solution lie in the
number field with defining polynomial $y^8 - 2y^7 + y^6 + 2y^5 - 10y^4 + 6y^3 + 9y^2 - 6y + 1$, which is not Galois.
Curiously, these algebraic numbers satisfy the simple linear relations $a+c+e = b+d,$ as well as $c-d = e-f$.
Edit: Tito Piezas III points out this first set of octics factor over $\sqrt2,$ and that the first relation immediately follows from
$$\begin{align}
a+c+\frac32 e &= 1+e^3\\
b+d+\frac12 e &= 1+e^3
\end{align}$$
which also implies the rather symmetric
$$\qquad\tfrac12(a - 3 b + c - 3 d) = -1+(a - b + c - d)^3$$
The second relation involving the edge length $f$, however, remains enigmatic.
II. $7$-cube
Next let's look at the case 3-simplex in 7-cube: Here the situation is similar:
If the $7$-cube is given as $[0, 1]^7$, then the coordinates are
$$ (0, 0, 0, a, 1, 1, 1) \\
(b, 0, 0, 1, 0, 0, 0) \\
(0, 1, 1, 0, c, 0, 0) \\
(1, 1, 1, d, e, 1, 1)
$$
where $a,b,c,d$ and $e$ are some algebraic numbers of degree 8. in fact, we have
$$\begin{align}
a &= \text{ zero near }0.2386303477\text{ of }\\ &x^8 - 12x^7 + 34x^6 - 36x^5 + 57x^4 - 32x^3 - 8x^2 - 64x + 16\\
b &= \text{ zero near }0.7308933837\text{ of }\\ &x^8 + 4x^7 - 42x^6 + 52x^5 - 103x^4 + 384x^3 - 424x^2 + 576x - 320\\
c &= \text{ zero near }0.7613696523\text{ of }\\ &x^8 + 4x^7 - 22x^6 + 28x^5 + 37x^4 - 152x^3 + 164x^2 - 44\\
d &= \text{ zero near }0.8560025785\text{ of }\\ &4x^8 - 20x^6 + 32x^5 - 87x^4 + 16x^3 + 124x^2 - 96x + 20\\
e &= \text{ zero near }0.1439974215\text{ of }\\ &4x^8 - 32x^7 + 92x^6 - 136x^5 + 53x^4 + 188x^3 - 218x^2 + 76x - 7\\
\end{align}$$
The edge length of this regular tetrahedron is the number $f = x\sqrt2 \approx 2.02827238$ where
$$\begin{align} x &= \text{ zero near }1.4342051606\text{ of }\qquad\\ &x^8 + 8x^7 - 14x^6 - 88x^5 - 11x^4 + 160x^3 + 44x^2 - 32x + 68.\qquad
\end{align}$$
Curiously, the algebraic numbers satisfy the relation $a+c = d+e.$
Edit: Tito Piezas III also pointed out this is actually $a+c = d+e = 1$, which re-phrases the question as to why their sum is unity.
Edit:
For all other cases I tried, the following patters seems to emerge: if $s_{(3,d)}$ is the maximal side length of the regular 3-simplex inside the $d$-cube, then we have
$$s^2_{(3, d)}\geq\begin{cases}\frac{2}{3}d &\text{ if }d=0 \pmod{3}\\ \frac{2}{3}d - \frac{13}{24} = \frac{2}{3}(d-1)+\frac{1}{8}&\text{ if }d=1 \pmod{3} \text{ and }d\geq 10\\ \frac{2}{3} d- \frac{5}{6} = \frac{2}{3}(d-2)+\frac{1}{2}&\text{ if }d=2 \pmod{3} \end{cases}$$
- For $d=3n$, coordinates are given by ($n\geq 1$)
$$
n\cdot(0,0,0)\\
n\cdot(0,1,1)\\
n\cdot (1,0,1)\\
n\cdot (1,1,0),$$
where '$n\cdot$' signifies $n$-fold concatenation.
- For $d=3n+1$, coordinates are given by ($n\geq 3$)
$$
( 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , \tfrac{1}{4} ) + (n-3)\cdot(0,0,0)\\
( 0 , 1 , \tfrac{3}{4} , 0 , 1 , 0 , 1 , 1 , 1 , 1) + (n-3)\cdot(0,1,1)\\
( 1 , \tfrac{1}{4}, 0, 1 , 1 , 1 , 1 , 1 , 0 , 0) +(n-3)\cdot(1,0,1)\\
( 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , \tfrac{3}{4} , 1 ,)+(n-3)\cdot(1,1,0),$$
where '$+$' signifies concatenation.
- For $d=3n+2$, coordinates are given by ($n\geq 1$)
$$
(0,0,\tfrac{1}{2}, 1, 1) + (n-1)\cdot(0,0,0)\\
(0,1,1,0,\tfrac{1}{2})+(n-1)\cdot(0,1,1)\\
(1,\tfrac{1}{2}, 1, 1, 0)+ (n-1)\cdot (1,0,1)\\
(\tfrac{1}{2},0,0,0,0) +(n-1)\cdot (1,1,0).$$
I conjecture that these values together with the values above for $s_{(3,4)}$ and $s_{(3,7)}$, are indeed the optimal values. It looks like there is again a $d\pmod{3}$ splitting of the result, and not a splitting $d\pmod{4}$, which is what you expected to see. Also the factor $\frac{3}{2}$ stays prominent.
Perhaps this would make a good new question for the Amer Math Monthly, after the case $k=2$ was solved.