4

Q. Does every (perhaps smooth) compact convex body $K$ in $\mathbb{R}^d$ admit a circumscribing simplex, each facet of which touches (shares a point with) $K$? How about a circumscribing regular simplex?

This question is inspired by this result (in a paper I have yet to access):

Shizuo Kakutani. "A proof that there exists a circumscribing cube around any bounded closed convex set in $\mathbb{R}^3$." Ann. Math., 43(4):739–741, 1942.

Perhaps the regular simplex question is answered already in $\mathbb{R}^2$? If so, I would appreciate a reference. Thanks!

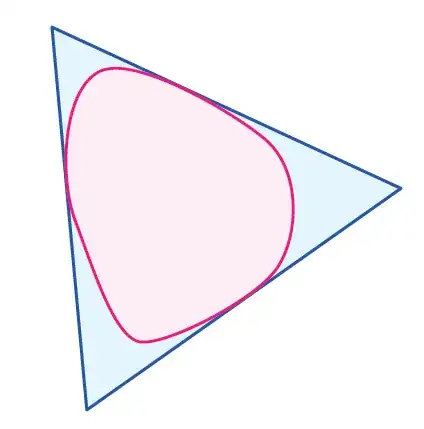
      EqTriCircum

Answered by Wlodzimierz Holsztynski in the comments: Yes, every $K$ has (many) circumscribing regular simplices.

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 1
    In $\ \mathbb R^2\ $ just move the lines till they touch the convex body. You can position your regular simplex (equilateral triangle) in every possible direction. – Włodzimierz Holsztyński Sep 06 '14 at 02:06
  • 5
    The same must be true in dimension $n$. When you move faces (each independently) of a regular simplex in parallel, the simplex stays regular (just make sure that the intersection of the chosen open half-spaces stays non-empty). – Włodzimierz Holsztyński Sep 06 '14 at 02:17
  • 1
    You may want to take a look at the references mentioned by Prof. Hatcher in his answer to the following question of mine: http://mathoverflow.net/questions/26318/points-on-a-sphere – José Hdz. Stgo. Sep 06 '14 at 02:21
  • 1
    I've just edited the link... – José Hdz. Stgo. Sep 06 '14 at 02:23
  • @WlodzimierzHolsztynski: "the simplex stays regular": Very nice!! – Joseph O'Rourke Sep 06 '14 at 02:29
  • 1
    Thank you Joseph. Indeed, in $\ \mathbb R^n,\ $ when one vertex is fixed, and we move the opposite opposite plane then according to Thales we get a homothetic simplex (hence regular if we started with a regular simplex). – Włodzimierz Holsztyński Sep 06 '14 at 02:40
  • @WlodzimierzHolsztynski: I like to believe that Thales would be pleased to be cited in this context, 2,500 years later. :-) – Joseph O'Rourke Sep 06 '14 at 02:43
  • 2
    I gave a bound for the volume of such a simplex in http://link.springer.com/article/10.1007%2Fs00013-014-0616-6 It is interesting to ask about regular simplex case. – Atsushi Kanazawa Sep 06 '14 at 04:43
  • 1
    Note the dual question:

    Q' Does every compact convex body $L$ in $\mathbb{R}^d$ admit an inscribed regular simplex, each vertex of which lies in the boundary of $L$ ?

    While Q admits the simple construction by moving planes described above, it is not obvious to me how the dual construction should work for the answer of Q'.

     – Pietro Majer Sep 06 '14 at 07:49
  • Precisely: it is not obvious (to me) that a simplex growing inside $L$ can in fact keep growing till all its vertices have reached the boundary of $L$. But the positive answer to Q implies a positive answer to Q' by duality, right? – Pietro Majer Sep 06 '14 at 07:55
  • @PietroMajer: I think what's missing here is that indeed the polar dual w.r.t. the simplex centroid maps to a simplex inscribed in the dual shape, but not all convex bodies can be obtained through this duality. – Joseph O'Rourke Sep 06 '14 at 13:32
  • Atsushi (above) proved: There is a simplex $S$ with Vol$(S) \le ;d^{d-1}$Vol$(K)$. – Joseph O'Rourke Sep 06 '14 at 17:38

0 Answers0