What are your favorite instructional counterexamples?

Question

Related: question #879, Most interesting mathematics mistake. But the intent of this question is more pedagogical.

In many branches of mathematics, it seems to me that a good counterexample can be worth just as much as a good theorem or lemma. The only branch where I think this is explicitly recognized in the literature is topology, where for example Munkres is careful to point out and discuss his favorite counterexamples in his book, and Counterexamples in Topology is quite famous. The art of coming up with counterexamples, especially minimal counterexamples, is in my mind an important one to cultivate, and perhaps it is not emphasized enough these days.

So: what are your favorite examples of counterexamples that really illuminate something about some aspect of a subject?

Bonus points if the counterexample is minimal in some sense, bonus points if you can make this sense rigorous, and extra bonus points if the counterexample was important enough to impact yours or someone else's research, especially if it was simple enough to present in an undergraduate textbook.

As usual, please limit yourself to one counterexample per answer.

Answer 1

The Fabius function, everywhere $C^\infty$, nowhere analytic.

see... sci.math post by G.A. Edgar, in thread “integral3”, Sep 9 2003

references:
J. Fabius, "A probabilistic example of a nowhere analytic $C^\infty$-function". Z. Wahrsch. Verw. Geb. 5 (1966) 173--174.

K. Stromberg, PROBABILITY FOR ANALYSTS (Chapman & Hall, 1994), pp. 117--120.

From the link:

Here is the construction of Fabius: Let $(X_k)$ be an iid sequence of random variables, each uniformly distributed on $[0,1]$. Let $X = \sum_{k=1}^\infty 2^{-k} X_k$. Let $Fb(x)$ be the cumulative distribution function of $X$. Check $Fb(x) = \int_0^{2x} Fb(t) dt$ for all $x \in [0,1/2]$.

Answer 2

The matrix $\left(\begin{smallmatrix}0 & 1\\ 0 & 0\end{smallmatrix}\right)$ has the following wonderful properties. (Feel free to add or edit; I can't remember all the reason I loathed it when I was learning linear algebra. It's funny how unexciting they all now seem, but it's a counterexample for almost every wrong linear algebra proof I tried to give.)

• Only zeroes as eigenvalues, but non-zero minimal polynomial (in particular, the minimal polynomial has bigger degree than the number of eigenvalues). Probably my favorite way to state this fact: the minimal polynomial is not irreducible or square-free. The same thing in a fancier language: the Jordan canonical form is not diagonal.

• Not diagonalizable, even over an algebraically closed field.

• Not divisible over $\mathbb C$. There are no matrices $M$ and integers $n\ge2$ so that $M^n = \left(\begin{smallmatrix}0 & 1\\\ 0 & 0\end{smallmatrix}\right).$ All diagonalizable and most non-diagonalizable complex matrices have $n$th roots.

  (This is because, if there was a square root, it'd have minimal polynomial x⁴, but since it's a two-by-two matrix, Cayley-Hamilton implies that the characteristic polynomial has degree 2).

• The matrix is nilpotent but not zero.

• It's one of the best examples when you need to remember why matrix multiplication is not commutative.

• Thinking of k² as a k[x]-module where x acts as this matrix should give wonderful (counter)-examples of modules for all the same reasons.

Also, $\left(\begin{smallmatrix}1 & 1\\ 0 & 1\end{smallmatrix}\right)$ is an example of an invertible matrix with the first three properties above. Its action on k² is in some sense the simplest example of a representation of a group ($\mathbb{Z}$) which is indecomposable but not irreducible.

Answer 3

A polynomial $p(x) \in \mathbb{Z}[x]$ is irreducible if it is irreducible $\bmod l$ for some prime $l$. This is an important and useful enough sufficient criterion for irreducibility that one might wonder whether it is necessary: in other words, if $p(x)$ is irreducible, is it necessarily irreducible $\bmod l$ for some prime $l$?

The answer is no. For example, the polynomial $p(x) = x^4 + 16$ is irreducible in $\mathbb{Z}[x]$, but reducible $\bmod l$ for every prime $l$. This is because for every odd prime $l$, one of $2, -2, -1$ is a quadratic residue. In the first case, $p(x) = (x^2 + 2 \sqrt{2} x + 4)(x^2 - 2 \sqrt{2} x + 4)$. In the second case, $p(x) = (x^2 + 2 \sqrt{-2} x - 4)(x^2 - 2 \sqrt{-2} x - 4)$. In the third case, $p(x) = (x^2 + 4i)(x^2 - 4i)$. This result can be thought of as a failure of a local-global principle, and the counterexample is minimal in the sense that the answer is yes for quadratic and cubic polynomials.

Answer 4

I like the double sequence $a_{nm} = \frac{n}{n+m}$ to show that $\lim_{n\to\infty}\lim_{m\to\infty} a_{nm}\neq \lim_{m\to\infty}\lim_{n\to\infty} a_{nm}$ .

Answer 5

A counter-example in graph theory - the Petersen graph.

_{(source: sdu.dk)}

In many ways it is the most simple graph with many strange properties. See the article on Wiki.

Quote from our professor who teaches graph theory:

If you think you've proved any lemma about graphs, try Petersen first!

Answer 6

The Cantor set is a nice source of counterexamples:

The first measure zero sets you meet are usually countable. However, the Cantor set is uncountable and measure zero.

It is totally disconnected, yet it is not a discrete space. In particular, this shows that connected components of a topological space need not be open sets.

Answer 7

The 8-element quaternion group. It can't be reconstructed from its character table (D_4 has the same one), and every subgroup is normal but it's not abelian.

Answer 8

I'm surprised no one mentioned the Hawaiian Earring:

_{(source: wikimedia.org)}

It's path-connected but not semi-locally simply connected (because any small neighborhood of the origin must contain a non-contractible loop). This implies many interesting properties, which make it a great counter-example. For instance...

• The Hawaiian Earring cannot have a universal cover.
• The Hawaiian Earring is not a CW-complex, although it is a compact, complete metric space
• An example of a space which is semi-locally simply connected and simply connected but is not locally simply connected is the cone on the Hawaiian Earring.
• For many years people thought the fundamental group was always a topological group. This turns out to be false, thanks to the Hawaiian Earring. There's a nice post about this here on MO
• This question is Community Wiki for a reason. I'm sure there are other examples of conjectures the Hawaiian Earring has disproven, so please add them!

Answer 9

The matrices $A=\begin{pmatrix} 17\times 11 + 1 & 25\times 11\\ 11^2 & 16\times 11 + 1 \end{pmatrix}$ and $B = \begin{pmatrix} 17\times 11 + 1 & 11 \\ 25\times 11^2 & 16\times 11 + 1 \end{pmatrix}$ are similar modulo $m$ for every positive integer $m$ but are not similar over the integers.

In other words, there exist matrices $X_m\in GL_2(\mathbf Z/m\mathbf Z)$ such that $X_mA \equiv BX_m \mod m$ for every $m$, but there does not exist a matrix $X\in GL_2(\mathbf Z)$ such that $XA = BX$.

This is due to Stebe, Conjugacy separability of groups of integer matrices. Proc. Amer. Math. Soc., 32:1–7, 1972.

Answer 10

The Weierstrass function - which I guess is a counterexample to the conjecture that a function which is continuous everywhere must be differentiable somewhere. I remember being pretty amazed when I first encountered it. It made me realize that continuity and differentiability are really different notions.

Answer 11

The basic fact that there are smooth non-analytic functions on $\mathbb R$, and that there are compactly supported smooth functions, is important in real analysis and functional analysis.

$f(x) =\begin{cases} \exp(-1/(1-x^2)),& x \in (-1,1) \\\ 0& \text {otherwise} \end{cases}$

The usual examples of these functions often seem contrived. Here are examples of smooth nowhere analytic functions.

Answer 12

I've always been fond of the popcorn function (aka Thomae's Function), which is given by $f\colon \mathbb{R} \to \mathbb{R}$ via

$f(x) = \begin{cases} \frac{1}{n} & \mbox{if } x = \frac{m}{n} \in \mathbb{Q} \\ 0 & \mbox{if } x \notin \mathbb{Q}. \end{cases}$

This function has a couple of amusing properties.

(1) It is upper semicontinuous on $\mathbb{R}$, yet has a dense set of discontinuities (every one of which is removable) (namely $\mathbb{Q})$.

(2) Since it is bounded and has a set of measure zero as its set of discontinuities, it is Riemann integrable. So if we consider $g(x) = \int_0^x f(t)\ dt$, we see that $g \equiv 0$, so that $g'(x) \not \hskip 2pt = f(x)$ on a dense set.

References: https://en.wikipedia.org/wiki/Thomae%27s_function and of course "Counterexamples in Analysis" (Sec 2.15-2.17)

Answer 13

Counterexamples are very important when a student learns how to think in intuitionistic logic (and he has already been "spoiled" by classical logic). The counterexamples destroy the classical intuition, and when properly explained they help the student understand how to think intuitionistically. Some that seem to work particularly well in my experience involve finite sets. Intuitionistically the following are not provable:

1. A subset of a finite set is finite.
2. The powerset of a finite set is finite.
3. If a subset of $\mathbb{N}$ is not finite then it is infinite.
4. The elements of a finite set may be listed without repetition.

All of these can be rescued with the additional assumption that the sets involved have decidable equality and that the subsets involved have decidable membership.

However, it does not really help the student to just know that certain "obvious" facts are not provable. He really needs to see how the "facts" can be false. The ones listed above are all false in the effective topos, but that's a complicated gadget for a beginner. It turns out informal explanations work well enough because most students know a little bit of programming. They just needs to know that the Halting Oracle does not exist.

My favorite counterexample in intuitionistic logic is that it is consistent to assume the so-called Axiom of Enumerability, which says that there are countably many countable subsets of $\mathbb{N}$. (Explanation: in the effective topos this just means that there is an effective enumeration of computably enumerable subsets of $\mathbb{N}$.) Many basic theorems of computability theory can be proved, phrased in a suitable form, from the axiom of enumerability using just constructive logic and no mention of machines of any kind.

Answer 14

Let $P dx + Q dy$ be a one-form, or if you're using the terminology of an introductory multivariable calculus course, a "vector field" that you can take line integrals of. Then students learn Green's Theorem, which says that if some countour $C$ bounds a region $D$, then $$\int_C P dx + Q dy = \int_D \left(\frac{dQ}{dx}-\frac{dP}{dy}\right) dx dy.$$

From this, one deduces that if the expression on the right hand side vanishes, then the integral around any contour is $0$. In particular, this allows one to define a primitive for $P dx + Q dy$.

Many students (myself included, a long way back) don't pay enough attention to the hypotheses in Green's Theorem and then assume that this is true of the following one-form (or "vector field"), which is my fundamental counterexample:

$$\frac{-ydx}{x^2+y^2} + \frac{xdy}{x^2+y^2}$$

Eventually a student discovers that the integral of this around the origin is $2 \pi$ and then wonders what went wrong. The problem is that the hypothesis of Green's Theorem requires that the form be defined everywhere in $D$.

In other words, this is a fundamental counterexample to the claim that a one-form in the plane with zero curl (where by "curl" I just mean the right hand side of the above) has a primitive.

Furthermore, this is a fundamental example of a nontrivial element in a de Rham cohomology group. In this case, the one-form above generates $H^1_{\text{dR}}(\mathbb{R}^2\setminus \{(0,0)\},\mathbb{R})$.

Answer 15

The Baumslag--Solitar groups have presentations

$BS(p,q)=\langle a,b\mid a^p=b^{-1}a^q b\rangle$.

They have the following nice properties:

1. they're two generator, one relator groups;
2. they can be written as an HNN extension of $\mathbb{Z}$ over $\mathbb{Z}$. (This means that they're constructed by 'gluing' $\mathbb{Z}$ to itself in some way.)

So from the point of view of combinatorial group theory, they could hardly be simpler. And yet, for suitable values of $p$ and $q$ (typically $p,q$ relatively prime integers greater than 1 will do), we find that:

1. they're non-Hopfian, meaning that they admit a self-epimorphism with non-trivial kernel;
2. hence they're not even residually finite;
3. they have exponential Dehn function (meaning that the word problem can be solved, but only very slowly);
4. their virtual first Betti number is one (meaning that every finite-index subgroup has abelianisation of rank one)...

I could go on.

Answer 16

Homotopy groups do not, in general, commute with sequential colimits, even for nice maps between nice spaces.

I just learned this beautiful example from Bill Dwyer.
Take the sequence

$S^1\stackrel{2}{\longrightarrow}S^1\stackrel{3}{\longrightarrow}S^1\stackrel{4}{\longrightarrow}\cdots.$

Here $n$ denotes the $n$th power map on $S^1$. Thinking of $S^1$ as $\mathbb{R}/\mathbb{Z}$, one finds that the colimit of this sequence (in the category of topological spaces) is the quotient group $\mathbb{R}/\mathbb{Q}$. Note that this quotient group, topologized as a quotient space of $\mathbb{R}$ by the relation $x\sim y$ if $x-y\in \mathbb{Q}$, has the indiscrete topology. In particular, the colimit of this sequence is a contractible topological space and has trivial homotopy groups.

On the other hand, the colimit of the corresponding sequence of fundamental groups is the group $\mathbb{Q}$ (checking this is a fun exercise).

(There's something sort of odd here, because one might have guessed that $\mathbb{R}/\mathbb{Q}$ would be a model for $K(\mathbb{Q}, 1)$, since after all $\mathbb{R}$ is a free $\mathbb{Q}$-space. But there are no interesting open sets in the quotient and hence no chance of local triviality.)

Answer 17

A standard result in introductory calculus classes is that, if a function has positive derivative on an open interval, then it's increasing there.

Based on this, students tend to think that, if $f'(a)>0$, then $f$ must be increasing "near $a$."

However, the example $f(x) = 2x^2\sin(1/x)+x$ (set $f(0)=0$) shows that this is quite false!

Answer 18

A basic result in commutative algebra asserts that direct limits commute with tensor products. My favourite counterexample to the statement obtained by replacing "direct" with "inverse" is the following. Let $p$ be a prime number; then

$\bigl(\varprojlim_n\mathbb Z/p^n\mathbb Z\bigr)\otimes_{\mathbb Z}\mathbb Q\cong\mathbb Q_p$,

the field of $p$-adic numbers (completion of $\mathbb Q$ with respect to the metric induced by the $p$-adic valuation), while

$\varprojlim_n\bigl((\mathbb Z/p^n\mathbb Z)\otimes_{\mathbb Z}\mathbb Q\bigr)=0$,

since every $\mathbb Z/p^n\mathbb Z$ is torsion and $\mathbb Q$ is divisible.

Answer 19

The Poincaré homology sphere, a spherical 3-manifold with fundamental group the binary isosahedral group, was Poincaré's counterexample to the original formulation (in terms of homology) of his conjecture. Due to its countless descriptions -- as a spherical 3-manifold, via Dehn surgery, as the configuration space of an isosahedron, etc -- it's still a motivational example in geometry and topology.

Answer 20

Added in edit. To understand this answer, one needs a definition that is current in French but for which I have not found a clearly equivalent word in English (causing misunderstandings, as can be seen in the comments). One says that a function $f$ defined near $0$ (say) has a "développement limité" (DL, which could be translated by "restricted expansion") of order $n$ at $0$ if there are numbers $a_0,a_1,\dots, a_n$ such that

$$ f(x) = a_0+a_1 x+a_2 x^2 + \dots + a_n x^n + o_{x\to 0}(x^n). $$

My instructional counter-example is: (end of addition)

The function $x\mapsto x^3\sin(1/x)$ has a second-order DL (before edit: "Taylor series") but is not twice differentiable at $0$. The circumstances where I came across this example are too embarrassing to tell here...

Answer 21

I'd say the Tutte Graph, which is a counterexample to

Tait's conjecture: Every 3-connected cubic planar graph has a Hamiltonian cycle.

Initially, I thought this counterexample was extremely non-instructive, since I assumed that Tutte discovered it via some ingenious trial and error. But, after seeing a talk by Bill Cunningham, I discovered how Tutte came up with his counterexample and why it is a counterexample (it's unclear from looking at Tutte's graph that it is not Hamiltonian). The idea is quite simple but useful. Tutte assumed that Tait's conjecture was true and proceeded to prove a sequence of stronger (yet equivalent) conjectures. He then found a very small counterexample to the strongest conjecture, and then deconstructed the sequence of proofs to obtain a counterexample to Tait's conjecture.

I really like this method because it shows that there is hope for a mathematical caveman like me as long as I use my brain. That is, the counterexample was actually not pulled out of thin air like I initially thought.

Answer 22

The Moulton plane is a projective plane that is a counterexample to the Desargues theorem, the little Desargues theorem, and just about every "nice" property of projective planes.

Its discoverer, F.R. Moulton, is best known as an astronomer. He apparently came up with the Moulton plane after sitting in on a projective geometry course as a graduate student.

Answer 23

The blowup of $\mathbb{P}^2$ in the 9 points of intersection of two generic cubics admits infinitely many $(-1)$ curves. This example is very important in getting rid of the naif picture of algebraic surfaces.

Answer 24

Two common misconceptions that students have about the concept of independence in probability are

1) Thinking "$X$ and $Y$ are independent" means "$X$ and $Y$ don't affect each other".
2) Thinking "A set of variables is independent" means the same thing as "each pair of variables are independent.

A useful counterexample that addresses both of these misconceptions at once is as follows:

Let $X$ and $Z$ be independent random variables, each equally likely to be $1$ or $-1$. Let $Y=XZ$.

In this example, changing the value of $X$ clearly changes the value of $Y$, but it does not change the distribution of $Y$. So $X$ and $Y$ are independent even though they "affect each other" in some sense. Furthermore, the variables $X, Y, Z$ are pairwise independent, but not independent.

Answer 25

The alternating group on 4 letters is nice because it provides a counterexample to the converse of Lagrange's theorem: It has order 12, but it does not have a subgroup of order 6.

Answer 26

Finite topological spaces often provide nice and simple counterexamples in topology, including algebraic topology (check J. Barmak's thesis). After getting familiar with those spaces one easily comes up with examples of phenomena such as weakly homotopy equivalent spaces which are not homotopy equivalent (spaces consisting of 4 points and 6 points suffice) or homomorphisms between homology/homotopy groups that are not induced by continuous maps.

Of course, other counterexamples are available, but finite ones are certainly minimal in a sense.

Answer 27

Small's Example from noncommutative algebra...

The triangular ring $T = \pmatrix{\mathbb{Z} & \mathbb{Q} \\\ 0 & \mathbb{Q}}$ has the following properties:

• It's right noetherian but not left noetherian
• It's right hereditary but not left hereditary
• The right global dimension is 1 but the left global dimension is 2
• This generalizes to give an example of a ring with right global dimension $n$ and left global dimension $n+1$ by replacing $\mathbb{Z}$ by $R$, a commutative noetherian domain of global dimension $n$, then replacing $\mathbb{Q}$ by $K = Frac(R)$
• A similar example gives a ring which is noetherian but neither left nor right Ore. Just take $R = \pmatrix{S & 0 \\\ S & I}$ where $S = \pmatrix{\mathbb{Z} & 0 \\\ \mathbb{Z}_p & \mathbb{Z}_p}$ and $I = \pmatrix{\mathbb{Z} & 0 \\\ 0 & \mathbb{Z}_p}$ is an $S$-ideal.

Having been trained to think in a commutative world, I found the existence of an example for any one of these to be surprising. The fact that they were all (basically) the same example is even more amazing.

Answer 28

My favourite counterexample is purely academic: it does not have any applications, but I think it is pretty.

Let $X = \mathbb{N} \times \mathbb{N}$. Define a non-empty set $U \subseteq X$ to be open if for cofinitely many $x \in \mathbb{N}$ the set $\{ y \in \mathbb{N} \vert (x,y) \in U\}$ is cofinite.

Construct a sequence in $X$ that hits every point in $X$ exactly once. In other words, take a bijection $\mathbb{N} \rightarrow X$. Then:

• $X$ is countable;
• every point in $X$ is an accumulation point of this sequence, but
• the sequence has no convergent subsequences.

In particular, this is an example in a countable set that accumulation point of a sequence does not have to be a limit of a subsequence. I call this the Herreshoff topology for the (high-school) student of mine who came up with it. (I could not find it anywhere else, although I do not discard that I did not look hard enough.)

Answer 29

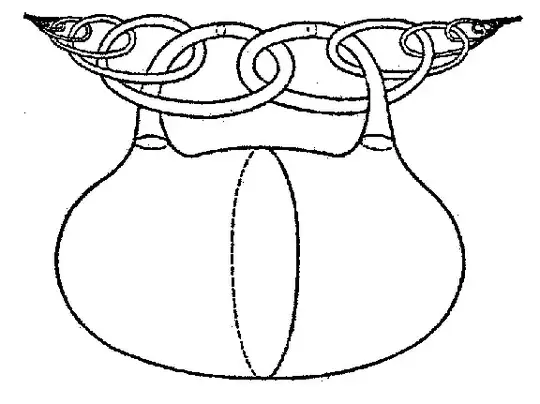
The Warsaw circle $W$ https://en.wikipedia.org/wiki/Continuum_%28topology%29 is a counterexample for quite a number of too naive statements.

The Warsaw circle can be defined as the subspace of the plane $R^2$ consisting of the graph of $y = \sin(1/x)$, for $x\in(0,1]$, the segment $[−1,1]$ in the $y$ axis, and an arc connecting $(1,\sin(1))$ and $(0,0)$ (which is otherwise disjoint from the graph and the segment).

Some observations: $W$ is weakly contractible (because a map from a locally path connected space cannot ''go over the bad point'').

Let $I$ denote the segment $[−1,1]$ in the $y$ axis. Then $W/I\cong S^1$ is just the usual circle, and thus we have a natural projection map $g:W \to S^1$. The point-preimages of $g$ are either points or, for a single point on $S^1$, a closed interval.

Thus the assumptions of the Vietoris-Begle mapping theorem hold for $g$, proving that $g$ induces an isomorphism in Cech cohomology. Thus the Cech cohomology of $W$ is that of $S^1$, but it has the singular homology of a point, by Hurewicz.

Since $I\to W$ is an embedding of compact Hausdorff spaces, we have an induced long exact sequence in (reduced) topological $K$-theory (see, for example, Atiyah's $K$-theory Proposition 2.4.4). Since $I$ is contractible, we get that $W$ and $S^1$ also have the same topological $K$-theory.

Note that the Warsaw circle is a compact metrizable space, being a bounded closed subspace of $R^2$. By looking on points on $I$ one sees that $W$ is not locally path-connected (and, in particular, not locally contractible).

The above observations imply:

1. A map with contractible point-inverses does not need to be a weak homotopy equivalence, even if both, source and target, are compact metric spaces. Assuming that the base and the preimages are finite CW complexes does not help.

2. The Vietoris-Begle Theorem is false for singular cohomology (in particular, the wikipedia version of that Theorem is not quite correct).

3. The embedding $I\to W$ cannot be a cofibration in any model structure on $Top$, where the weak equivalences are the weak homotopy equivalences and the interval $I$ is cofibrant. Because then we would have a cofiber sequence $I\to W\to S^1$ and thus also a long exact sequence in singular cohomology.

4. $W$ does not have the homotopy type of a CW complex (since it is not contractible).

5. Even though the map $g$ is trivial on fundamental groups, it does not lift to the universal cover $p: \mathbb{R} \to S^1$, because $g$ cannot be nullhomotopic. Thus the assumption of local path connectivity in the lifting theorem is necessary.

Answer 30

There exists a $3$-dimensional smooth projective variety $X$ which cannot be birational to a smooth variety with nef canonical bundle. This is because $K_X$ is big; if it was also nef it would have no cohomology and we could compute its self-intersection with Riemann-Roch by looking at the number of sections of its powers. It turns out that the self-intersection would be $3/2$.

This example (by Reid, I think) shows that if you want to have minimal models you have to allow singular varieties, so that $K_X$ can still be defined, but is not a Cartier divisor. This has led to the whole branch of birational geometry studying the type of singularities which are allowed in the minimal model program, like terminal, canonical, log-terminal, KLT and so on.

Answer 31

Coefficients of cyclotomic polynomials over $\mathbb{Q}$.

If you look at the factorization of $X^n-1$ over the integers, for $2 \leq n \leq 104$, you would "notice" that all nonzero coefficients of all factors are $\pm 1$. Indeed, $105$ is the first counterexample to this conjecture, with the 105th cyclotomic polynomial having coefficients of $2$ in its expansion. This can happen because $105$ has three distinct odd prime factors. The conjecture and the counterexample, however, are accessible even to high school students.

A quick Internet search suggests the following book as a reference:

McClellan, J. H. and Rader, C. Number Theory in Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1979.

I admit I have not read it - I first saw the counterexample while teaching high school, and it came up again in an advanced undergraduate course on Galois theory.

Answer 32

I like the Sorgenfrey line. It's finer than the metric topology on R, and hereditarily Lindelöf, hereditarily separable, first countable, but not second countable. It's non-orderable, but generalised orderable, etc. It's a popular example for metrisation theorems, e.g. All its compact subsets are at most countable.

Answer 33

The Schoenflies conjecture was asserting that the two connected components of the complement of an embedded $2$-sphere $S^2$ in $S^3$ were simply connected. A kind of generalized Jordan theorem.

Antoine's necklaces gave a first counterexample, and that counterexample was reworked by Alexander to obtain the horned sphere :

In this counterexample, the set of singular points of the embedding is a Cantor set, so is quite big. Later, Artin and Fox developed the notion of wild arcs, and found the following simpler counterexample, where there are only two singular points :

Answer 34

In question #14739, I asked whether the product of two ideals of a commutative ring $R$ could be defined lattice-theoretically the same way the sum and intersection can. Bjorn Poonen gave a great counterexample that shows the answer is no! This supports a point fpqc had been trying to make to me earlier that the relationship between $R$ and the Zariski topology on $\text{Spec } R$ was more subtle than I had thought: in particular, it has more structure than just the Galois connection.

Answer 35

The following are, I think, the "worst possible" counterexamples in measure theory. They would benefit from a nice list of properties -- I have a feeling that I'm forgetting a lot. Feel free to improve!

The Cantor set and its friend the Cantor function are standard counterexamples. Keeps increasing regardless of the zero derivative almost everywhere... Also, the corresponding measure $\mu$, defined so that the measure of the interval [a,b] is f(a)-f(b) where f is the Cantor function is supported on a Lebesgue-zero set.

Another good source of examples is the measurable set $A \subset [0,1]$ such that for any interval I, $\lambda(I\cap A) > 0$ and $\lambda(I\cap A^c) > 0$. ($\lambda$ is the Lebesgue measure, ^c denotes complement).

---

Here's a construction of A that I heard from Ulrik Buchholtz. Instead of just constructing A, we'll make two disjoint sets A and B which have intersection of positive measure with any interval. Consider the set of all subintervals of [0, 1] with rational endpoints. It is countable, so let I_n be the n-th interval in the list. Put two fat (positive-measure) disjoint Cantor sets (one for A and one for B) inside I₁. (We can just put the second inside some gap of the first). By the main property of Cantor sets, every interval I_n minus the Cantor sets is a non-empty union of intervals. So, we can put two fat disjoint Cantor sets (also disjoint from the previous ones) inside I₂, and keep going forever. Every time, we add one Cantor set to A and one to B.

Now, each subinterval of [0,1] will contain one of the I_n-s, and therefore its intersection with both A and B has positive measure. Both A and B are countable unions of measurable sets, and therefore measurable. We are done.

Answer 36

Volterra's function has a derivative everywhere which is bounded, discontinuous, and cannot be Riemann-integrated. It depends on the Cantor sets, of course, already mentioned.

Possible reference: Bernard R. Gelbaum, John M. H. Olmsted: Counterexamples in Analysis.

See also MO:Integrability of derivatives.

Answer 37

Writing $H$ for the Heaviside function, I was surprised when I first realised that the map $t \mapsto H(\cdot - t)$ is not Borel measurable as a map from $\mathbf{R}$ to $L^\infty(\mathbf{R})$. This illustrates that the intuition that "all unambiguously defined maps are measurable" really only works when the target space is separable.

Answer 38

As a counter-example for Fatou's lemma in measure theory: strict inequality can occure! Just take the measure space $\mathbb{N}$ with the counting measure and consider the functions \begin{equation} f_n(k) = \delta_{nk} \end{equation} Then the sum of $f_n$ is always $1$ while the pointwise limit of the $f_n$ will be the zero function having zero integral. If you have this counter-example then you do not need fancy measures and integrals at al to produce examples that in Fatou's lemma strict inequality may happen...

Answer 39

This is an easy one, but one I've found useful in the past to keep in mind, and which I've passed on to many younger students who are new to homological algebra. These students sometimes struggle with the idea of a non-free projective module because if you're new to modules and you still think of them via analogy to vector spaces then it's natural to think direct summands of free modules should be free.

A nice counter-example to keep in mind is the ring $\mathbb{Z}/6\mathbb{Z}$ and the projective but not free module $\mathbb{Z}/3\mathbb{Z}$ (projective because $\mathbb{Z}/6\mathbb{Z} \cong \mathbb{Z}/3\mathbb{Z} \oplus \mathbb{Z}/2\mathbb{Z}$)

Answer 40

"Every finitely-branching tree with infinitely many nodes has an infinite branch" is constructively false, as witnessed by the following counterexample:

https://math.andrej.com/wp-content/uploads/2006/05/kleene-tree.pdf

Andrej Bauer's exposition (above) is especially nice; most textbooks take a far less direct route to the result, which makes it harder to see what's really going on past the level of "yeah, the proof is correct step-by-step."

Answer 41

I occasionally use the following "counterexample" to unique factorization in Z in an introduction to math course: (1003)(1007)=(901)(1121). Once the students figure out what's going on, I think they learn something from it.

Answer 42

Ackermann function defined as

$ A(m, n) = \begin{cases} n+1 & \mbox{if } m = 0 \\ A(m-1, 1) & \mbox{if } m > 0 \mbox{ and } n = 0 \\ A(m-1, A(m, n-1)) & \mbox{if } m > 0 \mbox{ and } n > 0. \end{cases} $

is total recursive but not primitive recursive. To see this we could prove by induction on the complexity of primitive recursive functions that each primitive recursive function is eventually dominated by this function (we need a bit coding to keep the number of arguments consistent). Essentially this function manages to capture the ``fast-growing'' property. Note that the index set for recursive functions is not recursive while that for primitive recursive function is.

Answer 43

Any classical counter-example to inversion of a limit and an integral, $f_n:[0,1[\to\mathbb{R} ; x\mapsto n^2 x^n$ say. Basic, but important to motivate the dominated convergence theorem.

Answer 44

The statement S "every injective endomap is also surjective" can be formalized in terms of second-order logic (and, of course, precisely states that the structure in question is finite). This is a counterexample to any kind of compactness result for second-order logic, because if such a result existed, one would be able to get infinite sets satisfying S.

Answer 45

Here is a useful example of counter-examples in commutative ring theory;

Let $R=P(\mathbb{N})$ be the power set of $\mathbb{N}.$ It has a ring structure $(R, +, \times)$ where $+$ is the symmetric difference of sets and $\times$ is the intersection of sets.

Applications:

Obviously, $R$ is a commutative ring with $1$, ($\mathbb{N}$ is the $1$).

1) Let $R$ be a commutative ring with $1$ and a multiplicative closed set of $R$. If $R$ is Noetherian (Artinian) ring then $S^{-1}R$ is Noetherian (Artinian). Does the converse hold?

No, it doesn't.

Using the above example, for any prime ideal $p$ of $R$, $R_p$ (the localization at $p$) is Noetherian (Artinian) while, $R$ is not Noetherian (Artinian).

Outline:

Consider P({1}) $\subset$ P({1,2}) $\subset... $ and $P(\mathbb{N}) \supset$ P($\mathbb{N} \setminus${1}) $\supset$ P($\mathbb{N} \setminus${1,2}) $\supset ...$ showing that $R$ is neither Noetherian nor Artinian ring.

It is easy to verify that $R_p$ is isomorphic to $\mathbb{Z}/2$, hence it is both Noetherian & Artinian. (Every element of $R_p$ is either $0/1$ or a invertible.)

2) Let $R$ be an integral domain (also commutative with $1$), then for every multiplicative closed set of $R$, $S^{-1}R$ is an integral domain, hence for every $R_p.$ Does the converse hold?

By the above example, it doesn't, since $(P(\mathbb{N}),+,\times)$ is not an integral domain.

Answer 46

I'm shocked that noone has mentioned the Quaternion group! This thing is a counterexample to lots of basic questions you'd come up with while learning (finite) group theory.

For example (although not really a counterexample to a specific question), if you know the semidirect product construction and Sylow theorems and are trying to classify groups of low order, the quaternion group is the first group you can't construct as a semidirect product of cyclic groups. This can be an entry point for the extension problem for groups and cohomology of groups.

Answer 47

Assume given three projective systems $\{A_n,\alpha_{nm}\}_{n\in\mathbb{N}}$, $\{B_n,\beta_{nm}\}_{n\in\mathbb{N}}$ and $\{C_n,\kappa_{nm}\}_{n\in\mathbb{N}}$ of abelian groups (modules over some ring would equally do), endowed with arrrows $$ 0\rightarrow A_n\xrightarrow{f_n}B_n\xrightarrow{g_n}C_n\rightarrow 0 $$ making the above sequences exact for every $n$ and satisfying the commutativity conditions $\beta_{nm}\circ f_n=f_m\circ\alpha_{nm}$ and $\kappa_{nm}\circ f_n=f_m\circ\beta_{nm}$. Then one can form the projective limits of the system to find a sequence $$ 0\rightarrow \varprojlim A_n\xrightarrow{f}\varprojlim B_n \xrightarrow{g}\varprojlim C_n $$ and a classical result says that, in order for this sequence to be right-exact, one needs the system $A_n$ to be stationary - meaning that $\alpha_{nm}(A_n)=\alpha_{n'm}(A_{n'})\subseteq A_m$ for all $n,n'\gg m$.

A classical counterexample showing the necessity of this condition is to take $A_n=p^n\mathbb{Z}$ with $\alpha_{nm}$ given by inclusions, $B_n=\mathbb{Z}$ for all $n$ with identity maps $\beta_{nm}=\mathrm{id}$, and $C_n=\mathbb{Z}/p^n\mathbb{Z}$ with the obvious maps. The system $A_n$ is non-stationary because the image of $A_n$ in $A_m$ is $p^n\mathbb{Z}\subseteq p^m\mathbb{Z}$ which becomes smaller and smaller as $n\rightarrow \infty$: the corresponding sequence of projective limits is $$ 0\rightarrow 0\rightarrow \mathbb{Z}\rightarrow\mathbb{Z}_p $$ which is clearly not right exact.

[Later remark]: After typing all down, I remarked that everything can be found in Wikipedia at https://en.wikipedia.org/wiki/Inverse_limit Moreover, the stationary condition quoted above, usually referred to as Mittag-Leffler condition, is enough to prove right-exactness of $\varprojlim$ in Ab, but there is a counterexample due to Deligne and Neeman showing that in other categories this is not enough, see Link

Answer 48

My favorite counter-example is given in the short paper, "Almost Commuting Unitaries," by R. Exel and T. Loring.

Here is a little background. Two $n \times n$ matrices $A$ and $B$ are said to be "almost-commuting" if their commutator, $[A, B]$, is small in some matrix norm. In the paper, the authors exhibit a family of unitary matrices, $U_n$ and $V_n$ that "almost-commute" in the sense that given $\epsilon > 0$ there exists an $N \in \mathbb{N}$ with $|| [U_n, V_n] || < \epsilon$ for all $n \geq N$, yet for any commuting $n \times n$ matrices, $X, Y$ $(XY = YX)$ there exists an absolute constant $C > 0$ such that $\max(||X - U_n||, ||Y - V_n||) > C > 0$. This was one of the first counter-examples in a research paper that I understood because the authors method of proof is very elementary. The most technical fact used is that the winding number of a closed curve around the origin is a homotopy invariant.

Answer 49

Here is some simple counterexample in commutative algebra, which I found really cute when I first meet it:

Let $k$ be a field, $A = k[X_{1},X_{2},X_{3}\ldots],$ $I = (X_{1}, X_{2}^{2}, X_{3}^{3},\ldots)$ and $R = A/I.$ Then $\text{Spec}(R)$ consists of one point (because $\text{rad}(I)$ is maximal ideal of $A$); in particular $\text{Spec}(R)$ is a noetherian space, and $\dim R = 0$; although $R$ is not noetherian ring (since $\text{nil}(R)^{n}\neq 0$ for every $n$).

Answer 50

The matrix pencil $$ \left\{ \begin{bmatrix} 0 & 1 & x\\ 1 & 0 & 0\\ x & 0 & 0 \end{bmatrix} : x \in \mathbb{R} \right\}. $$ The matrices composing it are all singular, but they have no common left or right kernel (which is a property that one expects when first diving into the theory of matrix pencils). Singular pencils are difficult (or impossible) to handle for algorithms to solve generalized eigenvalue problems. For instance, Matlab's eig([0 1 0; 1 0 0; 0 0 0],[0 0 1; 0 0 0; 1 0 0]) returns 0 NaN 0 instead of something like NaN NaN NaN which would make more sense (no zero eigenvalues here), since the algorithm is not designed to handle this kind of singular problems.

Answer 51

Rotations $\rho_\alpha$ of the unit circle by an angle $2\pi\alpha$ are nice examples in the theory of discrete dynamical systems.

If $\alpha=m/n$ is rational, then every point on the circle is periodic of prime period $n$ for $\rho_\alpha$, but has no fixed points. This shows that Sharkowskii's theorem does not hold in general for functions continuous $f\colon X\to X$ if $X$ is not the real line or an interval of the real line.

If $\alpha$ is irrational, then the orbit under $\rho_\alpha$ of every point of the circle is dense, but $\rho_\alpha$ has nor sensitive dependence on initial conditions, and in particular is not caotic.

Answer 52

$\textbf{Algebra.}$

• The symmetric group $S_{3}$ is the first $\text{non-abelian}$ group and also this group has a fascinating property that $S_{3} \cong \mathscr{I}(S_{3})$ where $\mathscr{I}$ denotes the $\text{Inner - Automorphism}$ group.

• Example of a group which is $\textbf{isomorphic}$ to its proper subgroup. $\mathsf{Answer:}$ Take $G=(\mathbb{Z},+)$ and take $H= 2\mathbb{Z}$. Then $G \cong H$.

• Example of a free module in which a linearly independent subset cannot be extended to a basis. $\textbf{Answer.}$ As a $\mathbb{Z}$ module $\mathbb{Z}$ is free with basis $\{1\}$ and $\{-1\}$. Now $\{2\}$ is linearly independent over $\mathbb{Z}$. Note that $2$ cannot generate $\mathbb{Z}$ over $\mathbb{Z}$. If at all there is a basis $\mathscr{B}$ containing $2$, $\mathscr{B}$ should have atleast one more element, say $b$. We then have $b\cdot 2 - 2\cdot b =0$, i.e $\{2,b\}$ is linearly dependent subset of $\mathscr{B}$ which is absurd.

$\textbf{Analysis.}$

• The function defined by $f(x) = x^{2} \cdot \sin\frac{1}{x}$ for $x \neq 0$ and $f(x) =0$ for $x=0$. This is example of a function whose derivatives are not continuous.

• Set that is not Lebesgue measurable. Example given by Vitali.

Answer 53

The elliptic curve 960d1 in Cremona's tables is the smallest conductor example of an optimal elliptic curve with nontrivial Shafarevich-Tate group which is isogenous to an elliptic curve with trivial Shafarevich-Tate group.

Answer 54

I am surprised no one mentioned the unilateral shift on $l^2 ({\bf N})$, that is, $Te_i = e_{i+1}$ where $\{e_i\}$ is the standard orthonormal basis.

It provides examples for the following.

(a) a ring with elements $x,y$ such that $xy = 1 \neq yx$;

(b) an isometry from a Hilbert space to itself that is not a unitary;

(c) a one to one BLT that is not invertible;

(d) its adjoint is an onto BLT with nontrivial kernel;

and lots of other stuff (for example, its spectrum).

Answer 55

My favorite example in discrete mathematics is the sequence $1,2,4,8,16,31,..$. That is, number of regions in a circle after drawing all the chords between $n$ points on the boundary of the circle.

It shows that a simple pattern might be wrong, and that we do need formal proofs, no matter how many examples we've checked.

Answer 56

In the spirit of "examples do not prove anything in full generality (even if you have billions of them)", here is my favorite one: $\gcd(n^{17}+9,(n+1)^{17}+9)=1$ is true for all integers $1\leq n<8424432925592889329288 197322308900672459420460792433$, but false for $n=8424432925592889329288 197322308900672459420460792433$.

Answer 57

The 5-cycle $C_5$ is a great counterexample. It's the smallest imperfect graph, it's self-complementary, it has chromatic number $>\Delta$, it has no stable set meeting every maximum clique and yet satisfies $\omega = \frac{2}{3}(\Delta+1)$, it has chromatic number $> \frac 1 2 (\Delta+\omega+1)$, meaning that Reed's $\chi, \omega, \Delta$ conjecture is somehow tight.

And when you blow up each vertex into a clique or stable set of size $k$, the fun continues. For $k=3$ this gives you Catlin's counterexample to Hajos' Conjecture.

Answer 58

Not every epi is surjective

Recall that if $\mathcal{C}$ is a category, then an arrow $p:x\to y$ in $\mathcal{C}$ is said to be an epi if for every pair of parallel arrows $f,g:y\to z$ such that $f\circ p = g\circ p$, we have $f=g$. Of course, every surjective map is epi, but the converse is not true.

Consider the category of rings and ring homomorphism and the canonical injection of $\mathbb{Z}$ into $\mathbb{Q}$, call it $\iota$. Assume that $f,g:\mathbb{Q}\to R$ are two ring homomophisms such that $f\circ \iota=g\circ \iota$. Then $$ f\left(\frac{n}{m}\right) = f\left(\frac{n}{1}\right)f\left(\frac{m}{1}\right)^{-1} =(f\circ\iota)(n)(f\circ\iota)(m)^{-1} = g\left(\frac{n}{m}\right), $$ whence $\iota$ is an injective epi.

Answer 59

Peano Curve.

This provides a counter-example to an intuitive statement like

if $f:X\to Y$ is a continuous surjective map, then the dimension of $Y$ is less than or equal to that of $X$.

Answer 60

A nice counterexample to the statement "$L^p$ convergence to $0$ implies pointwise a.e. convergence to $0$" is obtained by taking characteristic functions of length $\frac{1}{n}$ wrapping around the interval $[0,1]$. These integrate to $\frac{1}{n}$, but converge nowhere to $0$ because the harmonic series diverges.

A counterexample to the converse is easier: just take $f_n = n(n+1)\chi_{[\frac{1}{n+1},\frac{1}{n}]}$. These integrate to $1$ and converge everywhere to $0$.

Answer 61

In topology, The comb space is an example of a path connected space which is not locally path connected. see https://en.wikipedia.org/wiki/Comb_space

Answer 62

In statistics not all distributions worth studying have mean, variance, skewness, or higher moments. Thus applications of the Central Limit Theorem may break down in such cases.

For example we have the Cauchy distribution:

$$f(x; x_0,\gamma) = \frac{1}{\pi\gamma \left[1 + \left(\frac{x - x_0}{\gamma}\right)^2\right]} = { 1 \over \pi \gamma } \left[ { \gamma^2 \over (x - x_0)^2 + \gamma^2 } \right],$$

with location parameter $x_0$ (=median/mode) and scale parameter $\gamma$ (=half width at half maximum).

The Cauchy distribution is also the distribution of the ratio of two variables $U$ and $V$, both of which are $\sim N(0,1)$. The moments do not converge.

Image from Wikipedia:

Answer 63

The four-color theorem is often expressed in different ways which are loosely claimed to be equivalent. However, not all of these formulations are actually equivalent, and not all of them are even true. This means that there are "counterexamples" to certain (incorrect) formulations of the four-color theorem.

The mathematically true statement of the theorem is:

(1) Any loopless planar graph can be colored with (at most) four colors such that no edge connects two vertices of the same color.

However, the theorem is usually introduced in the context of coloring maps, and is loosely framed as saying that "Any map can colored such that no two adjacent countries have the same color." However, making this formulation mathematically precise is surprisingly challenging. For example, here is a seemingly reasonable attempt to formalize the "map" version of the four-color theorem:

(2) Let $D$ be an open subset of the plane, and consider an arbitrary partition of $D$ into path-connected open subsets $S_i$ and their shared boundaries. It is possible to color each subset $S_i$ with one of four colors, such that the shared boundary of any two subsets $S_i$ that are assigned the same color consists only of isolated points.

However, it turns out that not only is proposition (2) not equivalent to proposition (1), but in fact (1) is true and (2) is false. Indeed, even even we further require that the boundaries of the subsets $S_i$ described in (2) consist only of straight line segments and right angles, the claim is still false. A counterexample - a partition of a rectangle into six subsets satisfying the requirements of (2) that cannot be four-colored - is given in https://www.jstor.org/stable/3647828.

This "counterexample" to the four-color theorem - really a counterexample to the incorrect version (2) - demonstrates the utility of formulating the theorem in terms of graph theory, where its statement is quite simple, rather than in terms of the motivating "map" version (which can be done, but requires a large number of fairly complex conditions).

Answer 64

I am quite keen of a counterexample in Strichartz estimates by Thomas Wolff that I think satisfies the requirements in your question. The problem was whether or not there are $L^p$ Strichartz estimates that lose no derivatives. Wolff gave a counterexample that, assuming the best control possible, then this is not possible for $p>2$. It uses the result by Charles Fefferman that the disk multiplier $S_1$ is not bounded on $L^p,~p\neq 2$. This is brilliantly explained by Professor Tao in the Notice of the AMS article "From Rotating Needles to Stability of Waves: Emerging Connections Between Combinatorics, Analysis, and PDE". It goes (more-or-less) like this:

Let $B(0,1)$ denote the unit ball of centre $0$ and radius $1$. Wolff showed that the inequality \begin{equation*} ||u||_{L^p([1,2]\times \mathbb{R}^n)}\leq C||f||_{L^{\infty}(B(0,1))} \end{equation*} fails, for $f$ bounded on $B(0,1)$.

Wolff used a mixture of Kakeya tube constructions, and the manipulation of specially constructed waves consisting of bump and exponential functions adapted to the tubes.

Answer 65

The group algebras of non-isomorphic groups could be isomorphic.

The simplest such example is as follows. If $G_1$ and $G_2$ are the two non-isomorphic non-abelian groups of order $p^3$ for an odd prime $p$, then $\mathbb{Q}[G_i]$ for $i=1,2$ are isomorphic. This is indirectly mentioned in an earlier answer to a question regarding counterexamples in algebra.

If one wants examples with $\mathbb{Q}$ replaced by finite fields or even integers, then such groups have been found but are significantly more complicated.

Answer 66

From an earlier post: "The 8-element quaternion group. It can't be reconstructed from its character table (D_4 has the same one), and every subgroup is normal but it's not abelian."

Although the character tables for the dihedral group D of order 8 and the quaternion group Q of order 8 may seem the same, they are not. Using Adams operations on the representation rings for D and Q, it is possible to show that these representation rings are different as rings with operations (either lambda or Adams operations). These Adams operations are defined in a paper by Aityah and Tall, where it is shown how to calculate them directly from character tables.

Answer 67

I like "the deleted Tychonov plank" which is described in "Counterexamples in Topology".

This space provide us a pure algebraic counterexample:

A commutative ring is called a $Z$-ring if all its elements are zero divisors. At first glance, it seems that an extension of a $Z$-ring by a $Z$-ring is necessarily a $Z$ ring. But this space provides a counterexample. The reason is explained here.

https://arxiv.org/abs/1307.5836

To be honest, I spent a few weeks to give a (positive) proof for this ring-extension statment, but finaly I found this counterexample in the book "Counterexamples in Topology" which excited me a lot.

As a consequence of this post we ask:

Are there two $Z$-rings $R_{1}$ and $R_{2}$ such that for every short ring exact sequence $$0\to R_{1} \to S \to R_{2} \to 0$$ $S$ must be a $Z$-ring?

Answer 68

Another one of my favorite counter examples is $2\mathbb{Z}$ which is a RNG, or a ring without identity.

Answer 69

One might expect that for any function $f$ in the Hilbert space $L^2$ with orthonormal basis $\{ f_i \}$, the generalized Taylor series $$\sum_{j=1}^\infty \langle f, f_j \rangle f_j$$ converges pointwise to $f$ almost everywhere. Carleson's theorem gives that this is true for the standard Fourier basis of $L^2([0,1])$, but there exist uncountably many pairs of functions $g$ and orthonormal (ordered) bases $\{ f_i \}$ such that the generalized Fourier series above diverges pointwise almost everywhere, as discussed here.

Answer 70

For a function $f:\mathbb R^n\to\mathbb R^m$, it is possible for the directional derivatives in all directions to exist at a point without $f$ being continuous there, let alone differentiable. Let $f:\mathbb R^2\to\mathbb R$ be the characteristic function of the set $E=\{(x,y):y=x^2,x\neq0\}$, and consider the behaviour of $f$ near the origin.

I learnt this example from Andrew D. Hwang in this post.

Answer 71

The tensor product over a ring is not left exact

Consider the short exact sequence $0\to2\mathbb{Z}\to\mathbb{Z}\to\mathbb{Z}_2\to0$ and tensor it by $\mathbb{Z}_2$ over $\mathbb{Z}$. It is well-known that this produces the exact sequence $$2\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}_2 \to \mathbb{Z}_2 \to \mathbb{Z}_2\otimes_{\mathbb{Z}}\mathbb{Z}_2 \to 0$$ where the first arrow is the $0$ map even if $2\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}_2$ is non-zero (in particular, it cannot be injective).

Answer 72

Square root and square power are not inverse operations

In fact, $\sqrt{x^2}=|{x}|$, which is defined for every $x\in\mathbb{R}$, while $({\sqrt{x}})^2=x$ is defined only for $x\geq 0$.