Volume of specials sets on sphere $S^N$

Question

Suppose I'm given $m$ points $\{q_i\}$ on the sphere $S^N$. I want to get a lower/upper bound for the volume of the following sets with respect to uniform probability measure $\mathbb{P}$ on the sphere. Let $$ A_i = \{ x \in S^N : (q_i,x) > (q_j,x) ~\forall j \neq i \} $$ Is there (say) a formula for such a quantity in terms of the $q_i$? Suppose I know everything there is to know about the $q_i$, is there a general strategy for calculating such things?

Answer 1

On a 2-sphere, such regions are spherical polygons (each of the inequalities in the definition of $A_i$ gives you a half-sphere). The area of such a polygon is given by a formula using the sum of angles of the polygon. So I am afraid you will first have to construct these Voronoi polygons. There are some algorithms for that.

In higher dimensions, the situation must be worse.

Answer 2

To supplement Yuri's answer:

In response to the earlier MO question, Delaunay triangulations and convex hulls, I posted this image:

---

     
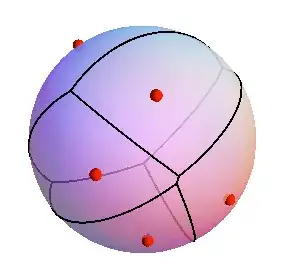
      ^{Image by Maxim Rytin in a Mathematica Demo.}

---

See that MO question for related references.