Minimizing the excursion of a sum of unit vectors

Question

I have $n$ unit-length vectors $v_i$ in $\mathbb{R}^3$, whose sum is zero: $$ v_1 + v_2 + \cdots + v_n = 0 \; .$$ Now I form the closed polygon $P$ in space by placing them head to tail. So the vertices of $P$ are $$ 0, v_1, (v_1+v_2), \ldots, (v_1+\cdots +v_{n-1}), 0 \; .$$ My question is:

What is the minimum excursion from the origin achievable by shuffling the vectors by a permutation of $(1,2,\ldots,n)$?

For example, the $12$ red vectors below wander $\sqrt{10}$ from the (purple) origin, but the light blue vectors—the same in a different order—stay within $\sqrt{3}$.
          
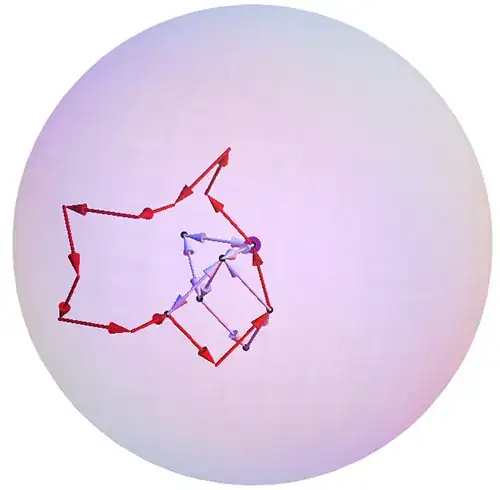
(These particular vectors derive from the vertices of a cuboctahedron, so some are negations of others.)

Is there some constant $r_{\min}$ independent of $n$ such that the sum can always be arranged to be at most $r_{\min}$, i.e., lie within an origin-centered ball of that radius? Or must $r_{\min}$ depend on $n$? Is there some natural algorithm for minimizing the excursion, or must I (in the worst case) try all $n!$ permutations?

Of course the same question can be asked in any dimension $\mathbb{R}^d$, but my focus is $\mathbb{R}^3$. Thanks for ideas and/or pointers!

Update1. The suggestion (in the comments) that $r_{\min} = \sqrt{d}$ in $\mathbb{R}^d$, based on an answer to the previous MO question, "Bounding a signed sum of complex numbers," is intriguing, and may be true. But I do not see that it is proved by that answer.

Update2. With key phrases suggested by Nik Weaver, I found a 1981 paper by Imre Bárány, "A Vector-Sum Theorem and its Application to Improving Flow Shop Guarantees" (Math. Oper. Res. link), which shows that $r_{\min} < \frac{3}{2} d$.

Answer 1

This is a famous open problem, $r_{\min}\le d$ is known as the Steinitz-lemma. It is conjectured that $r_{\min}= O(\sqrt d)$ but even $r_{\min}= o(d)$ is open. See also http://www.renyi.hu/~barany/cikkek/steinitz.pdf , section 3.