1

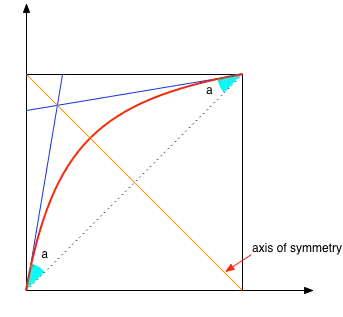
I need to design an analytical function that looks like this (See figure bellow). The idea is to control the angles "a" at the beginning and at the end. If the function depends on x (any kind of parameter, angle, value in [-1,1], etc.), we should have f(x) symmetric to f(-x) towards the line y=-x+1 (orange line). I mean, I should be able to build in some ways with the symmetric function. For instance, we have x^2 symmetric to x^(1/2).

I can build this function with a Bezier curve, but I need an analytical form that would give something close to the Bezier solution.

Thanks :)

enter image description here

Vincent Garcia
  • 111
  • 1

2 Answers2

1

A solution is a quadratic Bezier curve (a parabola), with control points $(0, 0)$, $(p, 1-p)$ and $(1, 1)$. The initial slope of this curve is $\frac{dy}{dx}=\frac{1-p}{p}=\tan(a+45°)$.

UPDATE: a more direct approach to the parabola.

Rotate the axis by $45°$ clockwise to make the axis of the parabola vertical. The equation is $v=\lambda u(\sqrt2-u)$, with the initial slope $\frac{dv}{du}=\lambda\sqrt2=\tan a$.

Then counter rotate using $u=\frac{x+y}{\sqrt2}$ and $v=\frac{y-x}{\sqrt2}$:

$$2(y-x)=\tan a(x+y)(2-x-y),$$

$$(\tan a)\ y^2\ +2(1-\tan a\ (1-x))\ y-(2x-\tan a\ x(2-x))=0.$$

  • I already use a Bezier curve, but the problem is that my solution provides me a set of (x,y) values. If I want to know the function value for a specific x, I need to interpolate between the two pairs (x_i,y_i) and (x{i+1}, y_{i+1}) when x_i < x < x_{i+1}. – Vincent Garcia Jun 14 '14 at 11:07
  • You can eliminate $t$ to get an implicit equation $f(x, y)=0$ - will be a conic -, andfrom ther an explicit relation $y=g(x)$ by solving the quadratic equation. –  Jun 14 '14 at 11:09
  • Sounds great. I'll give it a shot. Many thanks ! – Vincent Garcia Jun 14 '14 at 11:13
  • If I read you correctly, this means that for each $x$ value, I have to solve the equation to deduce $y$. Am I right? – Vincent Garcia Jun 14 '14 at 15:08
  • Right (you can precompute the expression for the solution). As long as $a<45°$, only one root is relevant. Double check my solution for possible sign errors. –  Jun 14 '14 at 15:12
  • The way I see it is that I'll have to compute one square root per $x$ value (among other things). Using a regular Bezier curve, I could use a simple linear interpolation which involves less consuming time operations. The problem with my approach is that I have a bunch of segments instead of a smooth curve. Knowing that there is an analytical solution is very nice and I think I'll try it. But I'm afraid that in the head, the interpolation will be preferable, even if I have to generate tones of intermediate points. Thank you @yves, I really appreciate your insight! – Vincent Garcia Jun 14 '14 at 17:36
  • If your concern is to draw the curve pixel by pixel very efficiently, then you can convert the implicit equation to integer numbers and use an incremental approach. Will cost you a few integer adds per pixel (!). If you want a sequence of line segments, or ($x, y)$ pairs, use the Bezier subdivision approach. –  Jun 14 '14 at 18:02
0

To simplify the solution, we assume that $0\le x\le 1$ and $0\le f(x)\le 1$. From your figure we obtain $f(0)=0$ and $f(1)=1$.

Now consider function $g(\xi)=f(\xi)-\xi$. We have $g(0)=g(1)=0$. It is represented by the red curve but viewed from a frame that the dotted line is the $\xi$-axis.

Setting $$g(\xi)=b+c \xi^2\text{ (1)}$$ and requiring that $$\frac{dg(\xi)}{d\xi}=\tan(a),\text{ } g(0)=0$$

We obtain: $$b=-\frac{\tan a}{2^{3/2}},\text{ }c=\frac{\tan a}{2^{1/2}}$$

Thus $f(x)=x+g(x)$ is probably the simplest curve that satisfies your criteria.

If you have other requirements, you may add higher order even terms in the expression (1).

mike
  • 5,604