How to evaluate the curvature by using normal gradient of a function?

Question

The gradient of the function $\phi$ is:

$$ \nabla\phi =(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z}) $$

and the unit normal is:

$$ \vec{N}=\frac{\nabla\phi}{|\nabla\phi|} $$

while the curvature can be defined as (I copy it from a book):

$$ \kappa =\nabla\cdot\vec{N}=\nabla\cdot(\frac{\nabla\phi}{|\nabla\phi|}) $$

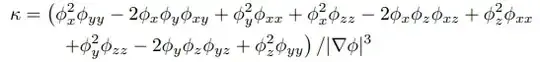
The book gives the answer like this which I have no idea how does it come out : enter image description here

I'm appreciate for the detailed explanation:-)

Have you tried expanding out the definition $\kappa = \nabla\cdot(\nabla\phi/|\nabla\phi|)$? Where did you get stuck? Try using the fact that $\nabla\cdot(\psi\vec A)=\vec A\cdot\nabla\psi + \psi\nabla\cdot\vec A$ where $\psi = 1/|\nabla\phi|$ and $\vec A=\nabla\phi$. — , Feb 27 '14 at 03:33
@Rahul Thanks for your tips, I think it can be solved now... — withparadox2, Feb 27 '14 at 05:03
Glad it helped! If you find the complete solution, feel free to post it as an answer to your own question for the benefit of other readers. — , Feb 27 '14 at 05:05

Semsem · Answer 1 · 2014-02-27T08:10:42.910

you have that $$\nabla\phi =(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z})\implies|\nabla\phi| =\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2}$$ Now we can write that $$\kappa =\nabla\cdot(\frac{\nabla\phi}{|\nabla\phi|}) \\=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})\cdot \frac{(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z})}{\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2}} \\=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})\cdot ( \frac{\frac{\partial\phi}{\partial x}}{\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2}},...,...) \\=\frac{\partial}{\partial x}( \frac{\frac{\partial\phi}{\partial x}}{\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2}})+\frac{\partial}{\partial y}(...)+... \\\\= \frac{\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2}\cdot\frac{\partial^2\phi}{\partial x^2}-\frac{\partial\phi}{\partial x}\cdot \frac{1}{2\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2}}\cdot(2\phi_x\phi_{xx}+2\phi_y\phi_{yx}+2\phi_z\phi_{zx})}{(\sqrt{(\frac{\partial\phi}{\partial x})^2+(\frac{\partial\phi}{\partial y})^2+(\frac{\partial\phi}{\partial z})^2})^2}+\frac{\partial}{\partial y}(...)+... \\= \frac{|\nabla\phi|\cdot\frac{\partial^2\phi}{\partial x^2}-\frac{\partial\phi}{\partial x}\cdot \frac{1}{2|\nabla\phi|}\cdot(2\phi_x\phi_{xx}+2\phi_y\phi_{yx}+2\phi_z\phi_{zx})}{|\nabla\phi|^2}+\frac{\partial}{\partial y}(...)+... \\= \frac{|\nabla\phi|^2\cdot\frac{\partial^2\phi}{\partial x^2}-\frac{\partial\phi}{\partial x}\cdot (\phi_x\phi_{xx}+\phi_y\phi_{yx}+\phi_z\phi_{zx})}{|\nabla\phi|^3}+\frac{\partial}{\partial y}(...)+... \\= \frac{(\phi_x^2+\phi_y^2+\phi_z^2)\cdot\frac{\partial^2\phi}{\partial x^2}-\frac{\partial\phi}{\partial x}\cdot (\phi_x\phi_{xx}+\phi_y\phi_{yx}+\phi_z\phi_{zx})}{|\nabla\phi|^3}+\frac{\partial}{\partial y}(...)+...$$ Now you can complete

How to evaluate the curvature by using normal gradient of a function?

1 Answers1