Estimation theory: Finding MSE and Variance of an Estimator

Question

Let $\hat{A}$ be an estimator of $A$ where $a<A<b$ and $\tilde{A}$ be another estimator such that$$\tilde{A} = \cases{a \text{ if } \hat A \leq a\\\hat A \text{ if } a< \hat A <b\\{b \text{ if } \hat A \geq b}}{}$$ How do I show that $\text{MSE}(\tilde A) \leq \text{MSE}(\hat A)$?
Given that $\hat A$ is an unbiased estimator of $A$, how do I show that $\mathbb{VAR}(\tilde A) \leq \mathbb{VAR} (\hat A)$?

Answer 1

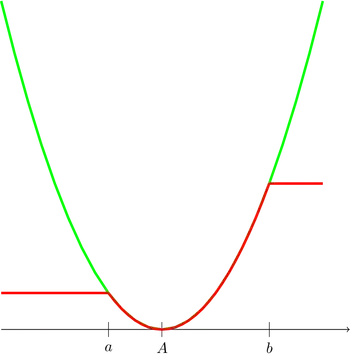
This follows from easy pointwise bounds, since $\widetilde A=a\vee \widehat A\wedge b$.

In the diagram the curve in red is the function $f(x)=([a\vee x\wedge b]-A)^2$, while the curve in green is $g(x)=(x-A)^2$. Since $f\leq g$ pointwise, we have $$(\widetilde A(\omega)-A)^2=f(\widehat A(\omega))\leq g(\widehat A(\omega))= (\widehat A(\omega)-A)^2$$ pointwise, so taking expectations gives

$$\mbox{MSE}(\widetilde A)=\mathbb{E}[(\widetilde A-A)^2]\leq \mathbb{E}[(\widehat A-A)^2]=\mbox{MSE}(\widehat A).$$

Answer 2

If $\hat{A}$ is an unbiased estimator of the true value $A$, then $\mbox{Bias}=\mathbb{E}[\hat{A}]-A=0$ and the $\mathbb{MSE}$ of $\hat{A}$ which is $\mathbb{E}[(\hat{A}-A)^2]$ is equal to $\mathbb{E}[(\hat{A}-\mathbb{E}[\hat{A}])^2]=\mbox{Var}[\hat{A}]$.

Let the sample space for the estimator $\hat{A}$ be $\Omega$, then we have either $\Omega=(a,b)$ or $\Omega\supset(a,b)$.

If $\Omega=(a,b)$: Obviously $\hat{A}=\tilde{A}$ almost everywhere and $\mathbb{VAR}[\hat{A}]=\mathbb{VAR}[\tilde{A}]$, so $\mathbb{MSE}[\hat{A}]\leq \mathbb{MSE}[\tilde{A}]$ holds.

If $\Omega\supset(a,b)$: Let $f:(a,b)\rightarrow \mathbb{R}$ be the density function of the estimator $\tilde{A}$ (assuming that your estimator is densitable). Since $\hat{A}=\tilde{A}$ for $a<\hat{A}<b$ and $\Omega/(a,b)$ is a non-empty measurable set $\hat{A}$ has a density $f/K$ for some $1<K<\infty$ on $a<w<b$. Let the density defined on $\Omega/(a,b)$ be $g:\Omega/(a,b)\rightarrow \mathbb{R}$ then $$K=\frac{1}{1-\int_{\Omega/(a,b)} g(w)\mbox{d}w}$$

Accordingly the variance of $\hat{A}$ and $\tilde{A}$ can be calculated as $$\hspace{-25mm}\mathbb{VAR}[\hat{A}]=\int_{\Omega/(a,b)}(w-A)^2g(w)\mbox{d}w+\frac{1}{K}\int_{(a,b)}(w-A)^2f(w)\mbox{d}w$$ $$\hspace{25mm}=\int_{\Omega/(a,b)}(w-A)^2g(w)\mbox{d}w+\left(1-\int_{\Omega/(a,b)}g(w)\mbox{d}w\right)\int_{(a,b)}(w-A)^2f(w)\mbox{d}w,$$ $$\hspace{-70mm}\mathbb{VAR}[\tilde{A}]=\int_{(a,b)}(w-A)^2f(w)\mbox{d}w$$

Let $k=\int_{\Omega/(a,b)}g(w)\mbox{d}w$ with $0<k<1$ then $$\hspace{-45mm}\mathbb{VAR}[\hat{A}]=\int_{\Omega/(a,b)}(w-A)^2g(w)\mbox{d}w+(1-k)\mathbb{VAR}[\tilde{A}]$$

Observe that $$\int_{\Omega/(a,b)}(w-A)^2g(w)\mbox{d}w\geq \int_{\Omega/(a,b)}(r-A)^2g(w)\mbox{d}w\quad\quad\quad (*)$$ for $r:=\arg\min_{a,b}{(|a-A|,|b-A|)}$ as a result we get

$$\hspace{-45mm}\mathbb{VAR}[\hat{A}]\geq \int_{\Omega/(a,b)}(r-A)^2g(w)\mbox{d}w+(1-k)\mathbb{VAR}[\tilde{A}]\\=k(r-A)^2+(1-k)\mathbb{VAR}[\tilde{A}]\\=\mathbb{VAR}[\tilde{A}]+k((r-A)^2-\mathbb{VAR}[\tilde{A}])$$

Using a similar argument as in $(*)$ and with the assumption that $(|a-A|=|b-A|)$ we have $$(r-A)^2\geq \mathbb{VAR}[\tilde{A}]$$ from where we get

$$\mathbb{VAR}[\hat{A}]\geq \mathbb{VAR}[\tilde{A}]+k\epsilon$$ for some $\epsilon>0$