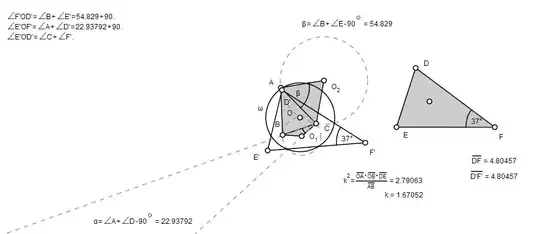
A little angle-chasing shows that the construction with isosceles triangles and circles through $C$ create a point $O$ such that
$$\angle BOC = A+D \qquad \angle COA = B+E \qquad \angle AOB = C+F$$
Because these values are symmetric in $(A,D)$, $(B,E)$, $(C,F)$, there's a corresponding point, $P$ for $\triangle DEF$ such that
$$\angle EPF = A+D \qquad \angle FPD = B+E \qquad \angle DPE = C+F$$
To save myself from typing a bunch of \primes, I'm going to move $\triangle DEF$ to coincide with $\triangle D^\prime E^\prime F^\prime$; that is, I take $P$ to coincide with $O$, and points $D$, $E$, $F$ lie on rays $\overrightarrow{OA}$, $\overrightarrow{OB}$, $\overrightarrow{OC}$.
Now, assuming inversion in the circle about $O$ with radius $k$ inverts $\triangle ABC$ to $\triangle DEF$, we have
$$k^2 = ad = be = cf$$
where $a := |OA|$, $d := |OD|$, etc.
Because $\angle AOB = \angle DOE = C+F$, the Law of Cosines implies
$$ \frac{a^2+b^2-|AB|^2}{2ab} = \cos(C+F) = \frac{d^2+e^2-|DE|^2}{2de}$$
so that
$$\begin{align}
de\left(\;a^2+b^2-|AB|^2 \;\right) &= ab\left(\;d^2+e^2-|DE|^2\;\right) \\
ad\cdot ae+ be\cdot bd - de|AB|^2 &= ad\cdot bd + be\cdot ae - ab |DE|^2 \\[4pt]
k^2 ae + k^2 bd - de |AB|^2 &= k^2 bd + k^2 ae - ab |DE|^2 \\[4pt]
ab|DE|^2 &= de|AB|^2
\end{align}$$
Multiplying through by $ab$, we get
$$a^2 b^2 |DE|^2 = ad\cdot be \cdot|AB|^2 \quad\to\quad a^2b^2|DE|^2 = k^4|AB|^2 \quad\to\quad k^2 = \frac{|OA||OB||DE|}{|AB|}$$
By the way, (I think) this is the "symmetric" formula for $k$:
$$k^2 = \frac{|AB|\;|BC|\;|CA|\;|DE|\;|EF|\;|FD|}{4\;\left(\; |\triangle PQR|^2 - (\; |\triangle ABC| - |\triangle DEF| \;)^2 \;\right)}$$
Here, $\triangle PQR$ is such that
$$|PQ|^2 = |AB|^2 + |DE|^2 \qquad |QR|^2 = |BC|^2 + |EF|^2 \qquad |RP|^2 = |CA|^2 + |FD|^2$$
The formula follows from this fact ...
$$|OA|^2 = \frac{|EF|^2\;|CA|^2\;|AB|^2}{4\;\left(\; |\triangle PQR|^2 - (\; |\triangle ABC| - |\triangle DEF| \;)^2 \;\right)}$$
... whose verification is left as an exercise to the reader.