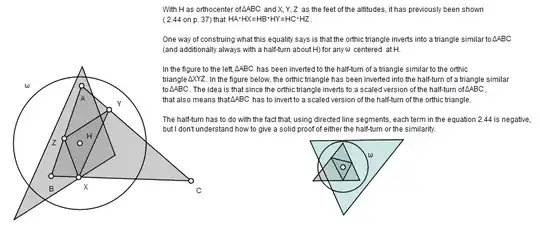
If the vertices of triangle $\Delta ABC$ are inverted about a circle $\omega$ centered at the orthocenter $H$ of $\Delta ABC$, the new triangle $\Delta A'B'C'$, is similar to the orthic triangle of $\Delta ABC$. Additionally it is rotated a half-turn about H. The diagram below shows this, however I am having trouble figuring out the proof, which is based on a separately derived equation (2.44) $$HX \cdot HA = HY \cdot HB = HZ \cdot HC.$$ (This is problem 5.3.4 of Geometry Revisited, Coxeter and Greitzer, and the equation 2.44 is on p. 37 of that book also).
Can anyone help supply the proof? I see that (2.44) is very close to saying that points A, B, C invert into X, Y, Z (but with a minus sign using directed segments), and that the minus sign accounts for the half-turn, but I don't see how to state this precisely.