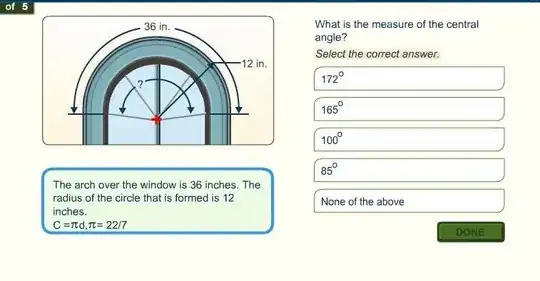
This is another grade school problem that's giving me trouble (posting on someone else's behalf).
I can see that a 36 inch semi-circumference yields a radius of 36/Pi or about 11.46 inches.
However, I can't see how to use this information to calculate the angle. Given the width of the arch, I may be able to do this, but don't see an easy solution otherwise.
Given that this is a grade school problem, I'm obviously missing something basic.
Using the "eyeball theorem" (ha ha), it seems like that angle is 172 degrees (it's clearly not 85 or 100 obviously).