In exercise 47 from Gauge Fields, Knots and Gravity by Baez and Munain, we want to show that if $\phi:M\to N$ is a map of smooth manifolds, then there is a unique pullback map on forms $$\phi^*:\Omega(N)\to \Omega(M)$$
that agrees with the pullback of 0-forms and 1-forms, is linear, and distributes over the wedge product (I've included an image since the TeX won't render here for some reason): 
My candidate definition for the pullback of a $k$-form was to say that 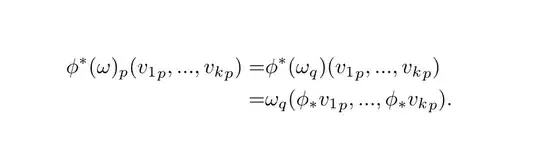
This seems to make sense, and resembles both the definition above for 1-forms and others I've found in other sources/questions here on MSE. However, I'm confused as to what the second linearity property would mean-- for example, if $\omega$ is a $k$-form and $\mu$ is a $p$-form and $k\neq p$, how can I use this definition when $\omega$ and $\mu$ act on different objects?
Would it be correct to say that elements of $\Omega(N)=\bigoplus_p \Omega^p (N)$ act on the tensor algebra $T(\text{Vect}(N))$ "homogeneously," i.e. so that for example $\omega+\mu$ where $\omega$ is a $k$-form and $\mu$ a $p$-form would act on $\text{Vect}(N)^{\otimes k} \bigoplus \text{Vect}(N)^{\otimes p}$ so that $\omega$ acts on the first summand and $\mu$ on the second?