The function $V(a)$ checks for lattice point visibility on the line $x+y=n$ from the origin:
\begin{gather} V(a) = \begin{cases} 1& \text{if }\mathrm{gcd}(a, n-a) = 1\\ 0&\text{otherwise} \end{cases} \end{gather}
Observe that Euler's Totient Function equals the number of visible lattice points
\begin{gather} \varphi(n) = 2 \sum_{a=1}^{\lfloor \frac{n-1}{2} \rfloor} V(a) \end{gather}
Example
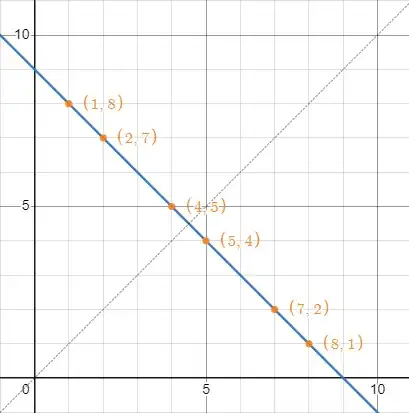
Consider the line $x+y=9$ with focus on these $3$ visible points
$\left(1,8\right),\left(2,7\right),\left(4,5\right)$
Notice due to the symmetry of the lattice points in the first quadrant with respect to the line $y=x$, we can multiply by $2$, so
$\varphi(9) = 6$
Question
Is this a correct formula
\begin{gather} \varphi(n) = 2 \sum_{a=1}^{\lfloor \frac{n-1}{2} \rfloor} V(a) \end{gather}
to equate the totient function $\varphi(n)$ to lattice point visibility?