0

I've been trying with no success to find a function as per title. What I mean by that is this:

Imagine a simple $\sin(x)$ function overlapped with an identical function, but traslated: $\sin(x+b)$.

The two functions define, at regular intervals, an area that is common under both curves. This increases from zero (when the two functions are out of phase by $\pi$) to $2$ (when the two functions coincide, if we integrate from $0$ to $\pi$).

Now, $\sin(x)$ and $\sin(x+b)$ were just an example. The area for them, as defined above, does NOT increase from $0$ to $2$ according to $\cos^2(b)$. Is it possible to find a function that does?

The actual numerical value for the area at each $b$ does not matter, but it must be exactly $\cos^2(b)$% of the maximum area at every $$b.

Jean Marie
  • 81,803
Leureka
  • 1
  • In your example the area increases, as you say, from $0$ to something, but in the case of $\cos^2(b)$ it should begin at $1$ not at $0$... and I don't see how it is possible... Don't you mean $\sin^2(b)$ ? – Jean Marie May 13 '23 at 13:28
  • Are you talking about the Autocorrelation? – user619894 May 13 '23 at 14:24
  • @JeanMarie no, when the two functions coincide (b=0) the area overlap is at maximum. I'm interested in a function where, as it increasingly moves out of phase, the area decreases until it reaches 0 at b=π/2. The actual numerical value for the area doesn't really matter, but the covered % must equal cos^2(b) of the maximum area. – Leureka May 13 '23 at 14:51
  • @user619894 I guess yes, I'm talking about autocorrelation. More specifically, i need to find the function that autocorrelates to the function cos^2(x). – Leureka May 13 '23 at 20:44
  • Look up the convolution theorem – user619894 May 14 '23 at 04:10
  • @user619894 i did. That doesn't make me able to calculate what I asked, i wouldn't know where to start to make an inverse Fourier transform of cos^2x. – Leureka May 14 '23 at 08:24
  • Ask mathstackexchange :) https://math.stackexchange.com/q/14389/617446 – user619894 May 14 '23 at 10:25
  • I have taken the liberty to add "autocorrelation" in your title, in order that it attracts the attention of further readers. Do you agree ? – Jean Marie May 18 '23 at 16:44
  • Sure no problem. – Leureka May 19 '23 at 10:04

1 Answers1

1

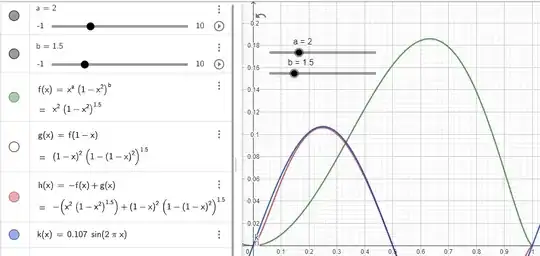
Elements giving a general methodology.

A fundamental observation is the connection of your autocorrelation issue with arclengths. Have a look at the following picture :

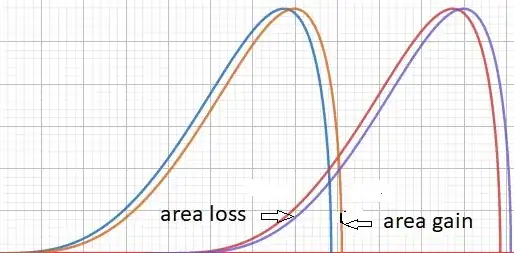
enter image description here

When moving from $a$ to $a+da$, the way the common area evolves is by considering gain minus loss, which amounts to lengths times $da$ (Cavalieri's principle), that you want to be equal to $da \cos(a)^2.$

$$da\left(\int_0^{a}\underbrace{\sqrt{1+\varphi'(x)^2}}_{L(x)}dx - \int_{\pi/2-a}^{\pi}\sqrt{1+\varphi'(x)^2}dx\right)= k da \cos(a)^2\tag{1}$$

where $k$ is a proportionnality factor (the formula for arc length computation can be found here).

Suppressing the common $da$ and differentiating with respect to $a$ gives :

$$L(a)-L(\tfrac{\pi}{2}-a)=-k \underbrace{2\sin(a)\cos(a)}_{\sin(2a)}\tag{2}$$

(Recall : derivation of $\int_0^{F(a)}f(x) \ dx$ with respect to $a$ is $f(F(a))F'(a)$)

Is it possible to find such a function $L$ ? By applying Laplace Transform to (2) which does not give an exact answer as far as I have attempted with Wolfram Alpha.

Let us assume that a function $L$ has been obtained (at least an approximation of it, see Edit below), what remains to be done ? Connecting functions $L$ and $\varphi$, i.e., obtain $\varphi$ by integration :

$$1+\varphi'(x)^2=L(x)^2 \iff \varphi(a)=\int_0^{a}\sqrt{L(x)^2-1} \ dx$$

Edit : In order to be convinced that it is possible to find a function $L$ verifying (2), have a look at the case given on the following figure (beware, the normalization is on interval $[0,1]$ instead of $[0, \pi/2]$) using a "Beta-like" function : there is an almost perfect agreement on the two thirds of interval $[0,1/2]$ of red and blue curves (see color meaning on the left).

enter image description here

Jean Marie
  • 81,803