Regular Polygon Inscribed In Circle - a question I found with no solution given. I made some progress but don't know how to proceed.

Question

Here is the full question:

A regular $48$-gon is inscribed in a circle with radius $1$. Let $X$ be the set of distances (not necessarily distinct) from the center of the circle to each side of the $48$-gon, and $Y$ be the set of distances (not necessarily distinct) from the center of the circle to each diagonal of the $48$-gon. Let $S$ be the union of $X$ and $Y$. What is the sum of the squares of all of the elements in $S$?

No solution was given, but I gave it a shot anyway.

Here's my answer so far:

First, we find the elements of set $X$ - the distances from the centre of the circle to each side of the $48$-gon. Let $x$ be the distance from the centre of the circle to one side of the polygon.

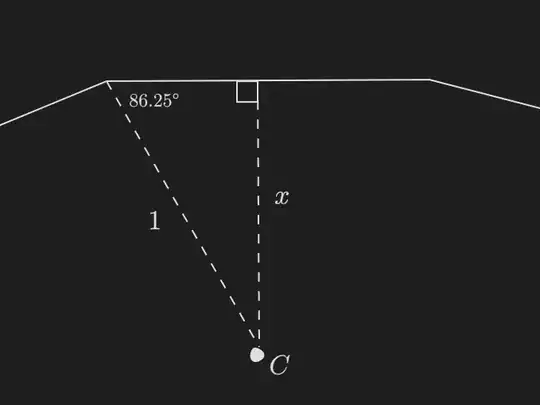
We draw this diagram (not to scale) and find out the following values.

A line from the centre of the $48$-gon, $C$, to one of its vertex is equivalent to the radius of the circle, which is $1$. This is the hypotenuse of the right-angled triangle.

That line is also an angle bisector of one of its interior angles. Each interior angle of the $48$-gon is $\frac{180°(48-2)}{48}=172.5°$, so $\frac{172.5°}{2}=86.25°$.

Now, we find that $x = \frac{\sin(86.25°)}{1} = \sin(\frac{23\pi}{48})$ in terms of radians.

As such, there are $48$ elements in set $X$, each element with the value of $\sin(\frac{23\pi}{48})$.

Second, we try to find the elements of set $Y$ - the distances from the centre of the circle to each diagonal of the $48$-gon. Here's where I get stuck.

We know that there are $\frac{48(48-3)}{2}=1080$ diagonals in the $48$-gon.

Since the polygon has an even number of sides ($48$ is even), there will be $\frac{48}{2}=24$ diagonals passing through the centre of the circle, meaning their distances from the centre will be $0$.

This leaves us with $1080-24=1056$ diagonals unaccounted for.

Now... how do I find every distance of the rest of the diagonals from the centre of the circle?

Is there anything wrong with my working so far? What suggestions do you guys have? How would you go about solving this question?

Thanks in advance!

Answer 1

For each of the $24$ main diagonals passing through the center there are $46$ vertices not on the diagonal. For each of those vertices, there are two diagonals (or one diagonal and an edge) connecting the vertex to an endpoint of the main diagonal. The distances from the center to these two diagonals are $\sin\theta$ and $\cos\theta$ for some $\theta$ and the sum of the squared distances is $\sin^2\theta+\cos^2\theta=1$, as shown.

This would give a total sum of $24\times 46=1104$, but since $24\times 46 \times 2=2208$ counts each of $1056$ diagonals and $48$ edges twice, the total sum desired is $$24\times 23=552$$

Answer 2

The problem is phrased strangely, but for a reason. The distances in set $X$ can also be conceptualized as distances to "diagonals," in the sense that a "diagonal" can be defined as a segment that joins any two distinct vertices, even if they are adjacent. When the vertices are adjacent, the resulting "diagonal" is not interior to the polygon.

Under this interpretation, the question can be posed more succinctly as follows:

For all pairs of distinct vertices of the $48$-gon, what is the sum of the squared distances from the center to the midpoint of the segment joining such pairs?

Then we can see that the solution can be readily found via the use of complex numbers: for each $k \in \{0, 1, \ldots, 47\}$, let $$v_k = e^{2\pi ik/48} = \cos \frac{k \pi}{24} + i \sin \frac{k \pi}{24}$$ be the complex coordinate of vertex $k$, which is a $48^{\rm th}$ root of unity. Then for each pair of distinct $j, k$, the midpoint of the segment joining vertices $j$ and $k$ is simply $$m_{j,k} = \frac{v_j + v_k}{2}.$$ The desired sum is therefore $$\begin{align} S &= \sum_{j = 0}^{46} \sum_{k = j+1}^{47} |m_{j,k}|^2 \\ &= \frac{1}{4} \sum_{j=0}^{46} \sum_{k=j+1}^{47} \left(\cos \frac{j \pi}{24} + \cos \frac{k \pi}{24}\right)^2 + \left(\sin \frac{j \pi}{24} + \sin \frac{k \pi}{24}\right)^2 \\ &= \sum_{j=0}^{46} \sum_{k=j+1}^{47} \cos^2 \frac{(k-j)\pi}{48} \\ &= \sum_{j=0}^{46} \sum_{k=1}^{47-j} \cos^2 \frac{k \pi}{48} \\ &= \sum_{j=0}^{46} \sum_{k=1}^{47-j} \frac{1}{2} \left(1 + \cos \frac{k \pi}{24}\right). \end{align}$$

I leave the rest of the computation as an exercise for the reader.

Answer 3

The vertices of a regular $n$-gon inscribed in the unit circle are $\,\omega^k \,\big|\,_{k = 0, 1, \dots,n-1}\,$ where $\,\omega = e^{i\,2k\pi/n}\,$. The distance from the center to the segment between vertices $\,j, k\,$ is the distance to the midpoint of the chord $\,\Bigg|\dfrac{\omega^j + \omega^k}{2}\Bigg|\,$. Adding up all the squared distances:

$$ \require{cancel} \begin{align} S = \frac{1}{4} \sum_{j=0}^{n-1}\sum_{k=0}^{n-1} |\omega^j+\omega^k|^2 &= \frac{1}{4}\sum_{j=0}^{n-1}\sum_{k=0}^{n-1} (\omega^j+\omega^k)(\bar \omega^j + \bar\omega^k) \\ &= \frac{1}{4}\sum_{j=0}^{n-1}\sum_{k=0}^{n-1} (\underbrace{|\omega^j|^2 + |\omega^k|^2}_{=\,1+1 \;\;\text{because}\;\; |\omega|=1} + \omega^j\bar\omega^k + \bar\omega^j\omega^k\;\;) \\ &= \frac{1}{4}\sum_{j=0}^{n-1}\sum_{k=0}^{n-1}\,2 + \underbrace{\xcancel{\frac{1}{4}\sum_{j=0}^{n-1} \omega^j\left(\sum_{k=0}^{n-1}\bar\omega^k\right)} + \xcancel{\frac{1}{4}\sum_{j=0}^{n-1} \bar\omega^j\left(\sum_{k=0}^{n-1}\omega^k\right)}}_{=\,0\;\;\text{because}\;\;\sum \omega^k = \sum \bar \omega^k = 0} \\ &= \frac{n^2}{2} \end{align} $$

The sum $\,S\,$ includes the $\,n\,$ unit distances to vertices $\,j=k\,$, and it counts the rest of segments $\,j \ne k\,$ twice, so correcting for those, the answer is:

$$ \frac{S - n}{2} = \frac{n(n-2)}{4} $$