In the context of determining pore volumes in adsorbing materials, I'm trying to find the pores that a gas molecule can go through. To do so, I need to solve a geometry/linear algebra problem. Here is a figure representing the problem. 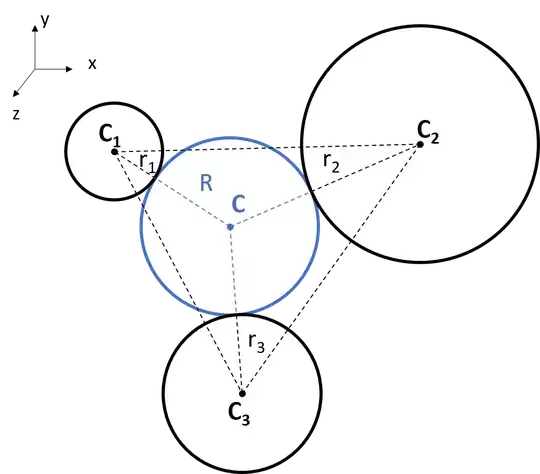
There are three circles with center coordinates C1, C2, and C3 with a radius r1, r2, r3, and I would like to calculate the radius of the circle, R, that is inside and touching the three circles at coordinate C. Note that $C, C_1, C_2 , C_3 \in \mathbb{R}^3$
I have already gotten a great answer for a similar case. but it was for spheres in 3D, not circles in 3D. Based on this answer solution for 2D case can be derived.
$A = \begin{bmatrix} (C_1 - C_2)^T \\ (C_1 - C_3)^T \end{bmatrix}$
$b = \begin{bmatrix} r_2 - r_1 \\ r_3 - r_1 \end{bmatrix}$
$c = \dfrac{1}{2} \begin{bmatrix} r_2^2 - r_1^2 - \| C_1 - C_2 \|^2 \\ r_3^2 - r_1^2 - \| C_1 - C_3 \|^2 \end{bmatrix}$
And we can solve the quadratic equation to get R: $R^2 + 2 R r_1 + r_1^2 = R^2 \bigg( b^T A^{-T}A^{-1} b \bigg) + 2 R \bigg( b^T A^{-T} A^{-1} c \bigg) + \bigg( c^T A^{-T} A^{-1} c \bigg)$
But this equation is only for 2D and not for 3D. If I apply this equation for the 3D case, $A \in \mathbb{R}^{2\times3}$, so I cannot calculate $A^{-1}$ as it is not a square matrix. I could rotate the plane so that values in one axis is 0, but I'm wondering if there is a more concise calculation.