(See also Edit 1 below).
We will fix $a,b$ and denote $P_{\delta}=P_{\delta}(a,b)$.
A first remark is that
$$\delta_1 < \delta_2 \ \implies \ P_{\delta_1} \supset P_{\delta_2}\tag{1}$$
Indeed, this is an immediate consequence of the fact that, for a given point $X$, if $\delta_1 < \delta_2 $,
$$\delta_1 \|x-a\|+\|x-b\|<\|a-b\| \ \implies \ \delta_2 \|x-a\|+\|x-b\|<\|a-b\| $$
Let us work on frontier curves $\partial P_{\delta}$ defined by :
$$\delta \|x-a\|+\|x-b\|=\|a-b\|$$
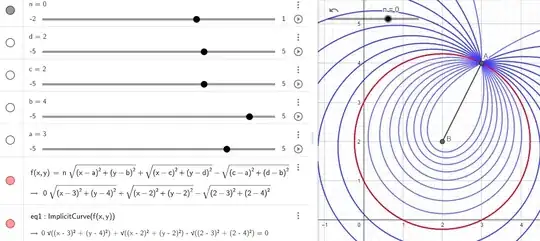
Here is an answer to part iii) in the planar case for different values of $\delta$ displayed with a stepsize equal to $0.1$.
As established in (1), these sets constitute a descending chain like russian dolls (see figure) with
$$-1 < \delta < 1$$
- For the range of values
$$0 \le \delta
< 1,$$
one gets convex sets:
For $\delta=0$ : it is the interior of the circle centered in $b$ with radius $b-a$ (displayed in red); all the other domains, for $\delta = 0.1, 0.2,$ etc. are interior to this circle, till $\delta=0.9$, the interior of the smallest petal. The case $\lambda=1$ corresponds to the interior of line segment $BA$ (case of equality $BM+MA=BA$ in the triangular inequality), this interior being void...
- Whereas for the complementary range of values :
$$ -1 < \delta <0,$$
sets $P_{\delta}$ are still non void but none of them convex
completing the previous ones to make "limaçon" frontier curves (proof below in the "Edit" part) ; all of them are exterior to the red circle.
Please note the way the frontier is gradually pinched in point $a$.
Edit 1 : We can also answer to question ii). The definition of $P_{\delta}$ involving only mutual distances, one can use a translation and a rotation such that point $a$ is placed at the origin and $b$ is placed at abscissa $b>0$ on the $x$ axis, without loss of generality.
This will allow to use polar coordinates for the current point
$$x=(r \cos \theta, r \sin \theta) \in P_{\delta}.\tag{2}$$
As $a=0$, the constraint becomes:
$$\delta \|x\|+\|x-b\| < \|b\| \tag{3}$$
(3) can be written, taking (2) into account :
$$\delta r + \sqrt{b^2+r^2-2br \cos(\theta)}<1$$
which is equivalent (under the condition $1-\delta r > 0$) to:
$$b^2+r^2-2br \cos(\theta)<(1-\delta r)^2$$
itself equivalent to:
$$r < \underbrace{\frac{2b}{\delta^2-1}(\delta-\cos(\theta))}_{\rho(\theta)}\tag{4}$$
which can be described as the interior of the internal loop (in blue) of a "limaçon", as said earlier, and it is convex (see explanation at the bottom of this answer).
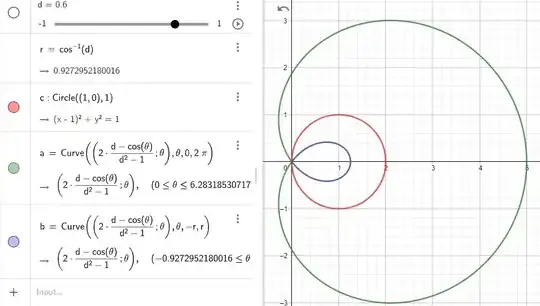
Please note that, in order to keep $r \ge 0$, the range of polar angle $\theta$ has to be :
$$\cos(\theta)\ge\delta \ \ \iff \ \ -\operatorname{acos}(\delta) \le \theta \le \operatorname{acos}(\delta)\tag{5}$$
Remark: extension to 3D is straightforward because it is the drop-like volume of revolution obtained by rotating the convex blue curve around $x$ axis, therefore itself convex.
Explanation about convexity: A classical convexity criteria for polar equations $\rho=\rho(\theta)$ is
$$\rho^2+2\rho'^2-\rho \rho'' \ge 0$$
(with $\rho$ given by (4)) because it amounts to condition
$$\delta(\delta-\cos \theta) \ge 0$$
which is verified indeed (see condition (5)) for the small loops.
See here
Edit 2: The limaçon curve is found in different cases. Here is an unexpected one connected to the "moiré" phenomenon, so striking that it is on the front cover of a book by a colleague that I give here:

It is obtained by the superposition of two identitical circular gratings, one slightly shifted with respect to the other.


