For the equiangular spiral $r=ae^{\theta \cot\alpha}$. Prove that the radius of curvature subtends a right angle at the pole . 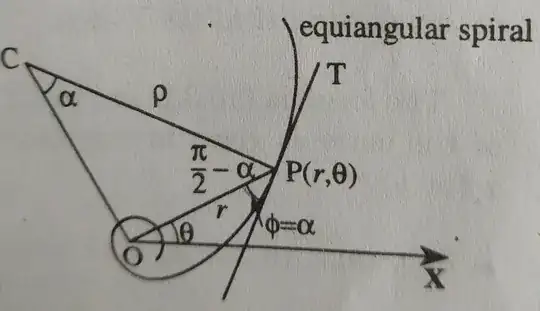
The solution given in the book is as follows:
We may easily deduce ,$\phi=\alpha$ and hence $\psi =\theta+\alpha$ so that $\frac{d\psi}{ds}=\frac{d\theta}{ds}$ and then $\rho=\frac{ds}{d\psi}=\frac{1}{\frac{d\psi}{ds}}=\frac{1}{\frac{d\theta}{ds}}=\sqrt{r^2+(\frac{dr}{d\theta})^2}=\sqrt{r^2+r^2\cot^2\alpha}=rcosec \alpha=r/sin\alpha$[since, $ds^2=dr^2+(rd\theta)^2$]. A glance at the above figure will now give the desired result, i.e $CP$ subtends a right angle $\angle COP$ at $O$.
However, I am not quite getting the solution. Firstly, did they assume $C$ to be the centre of the circle ? Next, did they consider the radius $\rho$ ? Now, we know that the curvature at all points in a circle is constant and is equal to $\frac{d\psi}{ds}=1/rho$ and hence , $\rho=\frac{ds}{d\psi}$ , isnt it? Did they first assume that $\angle{OCP}=\alpha$? And then, by using an elementary theorem on circles they deduced $\phi=\alpha$? After which they considered that tangent angle at $P$ to be $\psi=\theta +\alpha$? But when they differentiated, well, was $\alpha$ a constant ? If so, why was $\alpha$ a constant? Now, for the value of $\frac{1}{\frac{d\theta}{ds}}$ , how did they write it as $\sqrt{r^2+(\frac{dr}{d\theta})^2}$ ? Did they use the relation $ds^2=dr^2+(rd\theta)^2$ to derive that ? Does the same relation assures us that $\rho=\sqrt{r^2+r^2\cot^2\alpha}$ ? Finally , when $\rho =r/sin\alpha$, then $sin\alpha=r/\rho$ and hence $\angle{COP}=\frac{\pi}{2}$ , right? I am not quite getting it ...