6

Every Penrose tiling contains every valid finite patch of tiles, as shown e.g. in Theorem 8 here. So in order to figure out exactly which of the uncountably many Penrose tilings one is looking at, we must examine some infinite set of tiles - I'm curious which ones work. Some questions:

  • Does any infinite set of tiles uniquely determine the tiling? I think this is false, but I'm not positive.

  • If we have an infinite strip of tiles (i.e. the tiles obtained by crossing over opposite edges of successive rhombs), does that uniquely determine the tiling?

  • What about any sector of positive angle?

  • Any cofinite set? (This seems obviously true, but I'm not sure I know how to rule it out.)

RavenclawPrefect
  • 17,299
  • 2
    I don't have an answer, but it might be useful to know the terminology of the empire of a patch, which is the set of tiles which are completely determined, given a starting patch. So, your question can be reformulated as "What patches have the entire plane as its empire". Googling 'empire problem Penrose' should get you some resources to start. – Dan Rust Feb 08 '22 at 14:13
  • With regard to your first question, I remember reading that infinite 'worms' determine quite a bit of information, potentially the entire tiling. Or maybe one needs two intersecting worms (in different directions) to determine the entire tiling. – Dan Rust Feb 08 '22 at 14:20

1 Answers1

3

I'm going to refer to content from this book: Tilings and Patterns by Branko Grunbaum, Geoffrey C. Shephard (borrow for free with this link)

My answer will use the "kites and darts" Penrose tiling.

The Penrose tiles can be marked with lines that form infinite straight lines through the entire tiling. These lines are called Ammann bars. There are 5 sets of Ammann bars for a tiling, angled at multiples of 72 degrees to each other. There are only two possible distances between consecutive Ammann bars, and the ratio of those distances is Φ (the golden ratio, 1.618...). A sequence of distances between consecutive Ammann bars can be written as LSLLS (e.g.), for (L)ong and (S)hort.

Two very similar tilings

In this section I'll construct two Penrose tilings that differ only within a narrow strip that's infinitely long. So I think the answers the first 3 questions is "no", if I get to pick the infinite set.

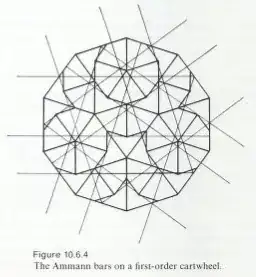
enter image description here

The book shows the above diagram

enter image description here

and describes how a valid set of Ammann bars can be constructed. (In this construction the sequence is palindromic, except for the S and L in the center). (Note that the "cartwheel" above has an S and L in all 5 directions, and the sequence will be extended as shown in 10.6.6.)

enter image description here

Here is the "cartwheel" rotated 90 degrees, with Ammann bars shown. The central L and S Amman intervals are shaded darker. Outside of these central intervals, the Ammann bars are symmetric, and therefore this tiling has 10-fold rotational symmetric, if you ignore the shaded portion.

enter image description here

In fact, you can rotate this tiling 108 degrees counterclockwise, and only one Ammann bar is affected, so only a single strip of tiles is affected. It seems this is a Conway worm that's being flipped.

Is my example a special case?

I think my example here might be a special case. I think there is only one sequence of Ls and Ss where single Ammann bar can be moved. In my example, all 5 sets of Ammann bars have this single bar pass through the same region. I imagine there are other value Penrose tilings, but I'm not sure.

Pentagrid

from http://www.ams.org/publicoutreach/feature-column/fcarc-ribbons :

The result is that a pentagrid, determined by the 5-tuple $ > (\gamma_0,\gamma_1,\ldots,\gamma_4) $ , defines a Penrose tiling of the plane.

Perhaps more remarkably, de Bruijn has proven that every Penrose tiling results from a pentagrid.

So, a Penrose tiling can be defined by 5 real numbers.

Infinite strip

If we have an infinite strip of tiles (i.e. the tiles obtained by crossing over opposite edges of successive rhombs), does that uniquely determine the tiling?

You can pick an infinite strip parallel to the one in my GIF, and then the answer is no.

But how much of the tiling is forced?

For the Ammann bars parallel to the strip, only one Ammann bar forced. But the other 4 sets of Ammann bars are completely determined.

enter image description here

This forces a lot of tiles. For example, notice how there are only a handful of unique patterns that the Ammann bars make. Also, note that the small triangle always exactly determines the exact position of a "kite". I'm not sure of the exact region that is forced though.

Tom Sirgedas
  • 1,028
  • 10
  • 12