Suppose we have $X$ and $Y$ are jointly distributed with density of $2$ if $0 < x < y < 1$ (and $0$ otherwise). I'd like to find the PDF of the sum, $X + Y$.
I read the Jacobian method here: pdf of sum of two dependent random variables
and set $Z = X + Y, W = X$ to apply that method.
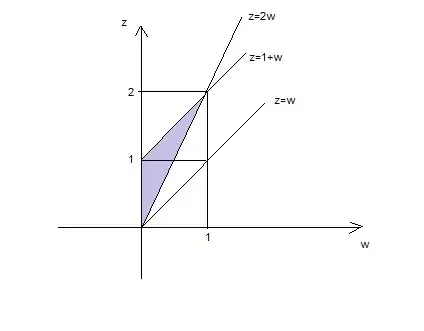
However, I am having trouble writing the bounds for the joint density function. I know that $0 < x < y < 1$ and thus $2x < z < 1 + x$, and since $w = x$ we know that $2w < z < 1 + w$ and $0 < w < z$.
Finally when I integrate the density function $2$ from $0$ to $z$ to find PDF of $Z$ the solution is simply...$2z$ for (what are the bounds?) How can I finish up the problem?