Recently I have been reading into Nuclear Fusion and the use of spherical tokamaks. My knowledge of maths and physics is quite limited, only a second year undergraduate level. I was wondering how I might obtain equations for the magnetic field around a simplified tokamak, namely a perfect torus.
I have derived the equation of a torus from the circle $$x^2+y^2=c^2$$ $$x(u)=c\cos(u), \ y(u)=c\sin(u), \ \ \ u \in [0,2\pi]$$ and another radial parameter $v$ by considering two circles of radius $a$ centred at $\pm c$ from the origin $$z(v)=a\sin(v), \ \ \ v\in[0,2\pi]$$ Shifting the $x$ and $y$ positions by: $a\cos(v)$ gives parametric equations of the form $$\begin{cases} x(u,v)=(c+a\cos(v))\cos(u)\\y(u,v)=(c+a\cos(v))\sin(u)\\z(u,v)=a\sin(v) \end{cases}$$ I know how to derive the formula for a magnetic field line in $\mathbb{R}^2$ and I assume it is fairly straightforward to do for $\mathbb{R}^3$. However, once I have the expression how can I deduce that the field lines should look like this?
$\hspace{4cm}$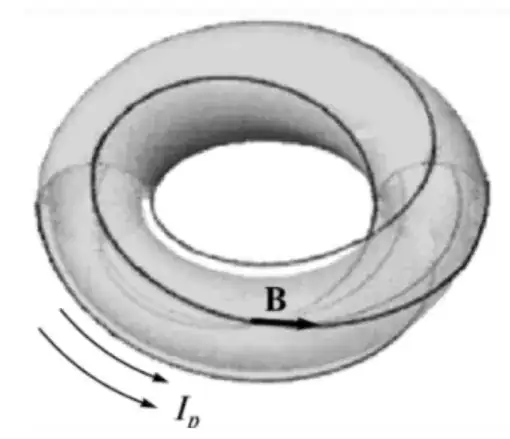
I have realised that it may be better to show that the magnetic field of a slice of the torus of infinitesimal thickness has a circular magnetic field, then revolve the circular magnetic field around the $\hat z$ axis to see it is a sort of helical spiral. If someone could advise on this I would greatly appreciate it.