1

Definition: A random variable (r.v.) is a numeric quantity that (i) takes different values with (ii) specified probabilities. [Notation: X, Y, Z, … (capital letters)]

(A random variable is a function from a sample space into the real numbers.)

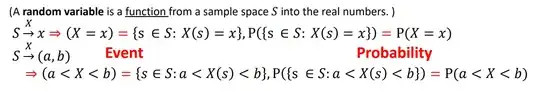
enter image description here

I am not sure I understand the meaning of the definition and especially the math equation showed above. Can anyone explain?

Graham Kemp
  • 129,094
Chi Tat Yu
  • 11
  • 1
    Did you try searching "math stack exchange random variable definition", and look at this post: What exactly is a random variable? If that doesn't answer your question, please edit your post to explain what part is unclear, so that someone doesn't have to explain it all from scratch. – Joe Oct 11 '21 at 02:11
  • I don't understand is the image. First S is sample base (for example: I throw a dice and get 1) Is the meaning for - X -> equal to put S in a function X? small x mean we get a real number x?

    and next it become (X = x) --> I partially get this, Mean the Capital X and small x mean the same thing?

     – Chi Tat Yu Oct 11 '21 at 03:09
  • Examples may help: (1) roll dice - the possible outcomes are discrete numbers. (2) weigh yourself - outcomes are from a continuous distribution around your average weight. – herb steinberg Oct 11 '21 at 03:14
  • 1
    The notation of probability is somewhat unique. Students are often used to $f$ for functions and $x$ for a variable, but a random variable *is* a function. It's also unique that a capital letter is used for the variable, and the same letter in lower case is used for a value that variable attains (a realization). – Joe Oct 11 '21 at 11:12
  • If $S$ is the sample space of three consecutive coin flips, and $X$ is the number of heads, then for example $X(HTH)=2$, and the notation in the picture says that $(X=2)={HHT,HTH,THH}$, so that $P(X=2)=P({HHT,HTH,THH})$, which if the coin flips were all fair would equal $3/8$. The main idea is that if you start with some probability space, which has a sample space and a probability measure on the events, then a "random variable" is a function from the sample space to the real numbers which pushes the probability measure forward to the real numbers. – Joe Oct 11 '21 at 11:21

0 Answers0