Eliminating $\theta$ from $\cos^3\theta +a\cos\theta =b$ and $\sin^3\theta +a\sin\theta =c$

Question

Eliminate $\theta$ from the equations. $$\cos^3\theta +a\cos\theta =b$$ $$\sin^3\theta +a\sin\theta =c$$

Can anyone solve this question?

Answer 1

$\def\¿{\mathcal}$ Maybe I am complicating this, yet another method.

I will use these identities:

$\cos^6x+\sin^6x=1-\frac34\sin^22x$

$\cos^6x-\sin^6x=\cos 2x(1-\frac14\sin^22x)$

$\cos^4x+\sin^4x=1-\frac12\sin^22x$

$\cos^4x-\sin^4x=\cos2x$

Let
$c=\cos x$,
$s=\sin x$,
$\¿ C=\cos 2x$,
$\¿S=\sin2x$

I use $d$ instead of $c$ in the original problem to avoid confusion.

Now we have $$c^3+ac=b\tag{1}$$ $$s^3+as=d\tag{2}$$

---

$\small\mathit{(1)^2+(2)^2}$, $$c^6+s^6+2a(c^4+s^4)+a^2(c^2+s^2)=b^2+d^2$$ $$\left(1-\frac34\¿S^2\right)+2a\left(1-\frac12\¿S^2\right)+a^2=b^2+d^2$$ $$\¿S^2=\frac{4\left[\left(a+1\right)^2-(b^2+d^2)\right]}{(3+4a)}$$

---

$\small\mathit{(1)^2-(2)^2}$, $$c^6-s^6+2a(c^4-s^4)+a^2(c^2-s^2)=b^2-d^2$$ $$\¿C\left(1-\frac14\¿S^2\right)+2a\¿C+a^2\¿C=b^2-d^2$$ $$\¿C\left[(a+1)^2-\frac14\¿S^2\right]=b^2-d^2$$ $$\¿C=\frac{(3+4a)(b^2-d^2)}{2(a+1)^2(2a+1)+(b^2+d^2)}$$ Now we can use $$\¿C^2+\¿S^2=1$$

Answer 2

So, if I understood properly your question, we have $$ \left\{ \begin{array}{l} \theta ,a,b,c \in R \\ \cos ^3 \theta + a\cos \theta - b = 0 \\ \sin ^3 \theta + a\sin \theta - c = 0 \\ \end{array} \right. $$ and we are looking for which domain of the four variables $ \theta ,a,b,c$ the system of the two equations has one or more (real) solutions.

Both equations are depressed cubics.

The discriminants are $$ \begin{array}{l} \Delta _1 = - 4a^3 - 27b^2 \\ \Delta _2 = - 4a^3 - 27c^2 \\ \end{array} $$ If

• $\Delta >0$ the equation has three distinct real roots;
• $\Delta = 0$ all roots are still real , and if $a=0$ gives three coincident roots, otherwise one simple root at $-3a/b; -3a/c$ and two coincident at $-3a/(2b) ; -3a/(2c)$;
• $\Delta < 0$ the equation has only one real root.

Then, denoting by $c_1, c_2, c_3$ the roots of the equation in $\cos$, eventually reduced to only two or one, and by $s_1, s_2, s_3$ those of the equation in $\sin$, you shall impose to have at least a couple for which $$ \left| {c_{\,k} } \right| \le 1\quad \wedge \quad \left| {s_{\,k} } \right| \le 1\quad \wedge \quad c_{\,k} ^2 + s_{\,k} ^2 = 1 $$

That means to write each cubic as the product of the three monomials $(x-c_k)$, etc. and patiently translate the above bounds and conditions onto $a,b,c$ by means of Vieta's formulas.

We get in fact $$ \left\{ \begin{array}{l} c_1 + c_2 + c_3 = 0 \\ c_1 c_2 + c_1 c_3 + c_2 c_3 = a \\ c_1 c_2 c_3 = b \\ \end{array} \right.\quad \Rightarrow \quad \left\{ \begin{array}{l} c_1 = - \left( {c_2 + c_3 } \right) \\ c_2 ^2 + c_2 c_3 + c_3 ^2 = \frac{3}{4}\left( {c_2 + c_3 } \right)^2 + \frac{1}{4}\left( {c_2 - c_3 } \right)^2 = - a \\ \left( {c_2 + c_3 } \right)c_2 c_3 = - b \\ \end{array} \right. $$ and similarly for the sine, changing $b$ with $c$.
So that, if the three solutions are real, the ellipse in the second line demand $a$ to be negative, resulting in the two curves are sketched below.

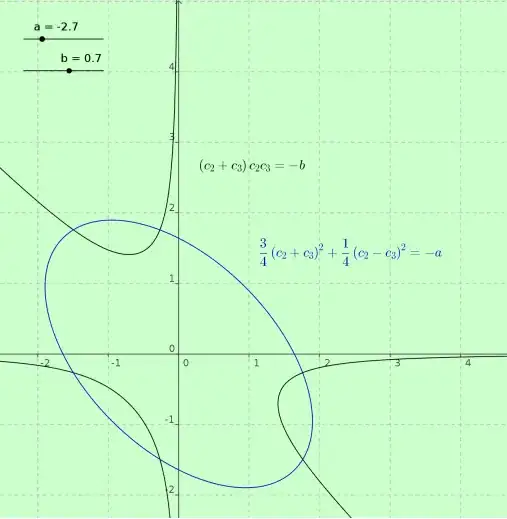
Note that, the properties of the cubic ensure that there is a minimum and maximum value for $b$ (in function of $a$) for which the two curves simultaneously touch each other, and such values are easy to determine imposing the tangency along $c_2 = c_3$.
And we shall impose that that point at least be within $[-1,1] $, etc.
Finally note that the intersection points are six, since we have not ordered the roots.

Answer 3

I have now my own answer developed out of conversation with David Quinn, so I thank him. I publish this answer to demonstrate the calculation. It seems to coincide with the calculation of Macavity in the comments above. Wow what a monster of a question.

We have $$x^3+ax=b$$ $$y^3+ay=c$$ Where $x^2+y^2=1$.

Adding and subtracting,

$$x^3+y^3+a(x+y)=b+c$$ $$x^3-y^3+a(x-y)=b-c$$

$$(x+y)(x^2-xy+y^2)+a(x+y)=b+c$$ $$(x-y)(x^2+xy+y^2)+a(x-y)=b-c$$

$$(x+y)(1-xy)+a(x+y)=b+c$$ $$(x-y)(1+xy)+a(x-y)=b-c$$

So $$(x+y)(1+a-xy)=b+c$$ $$(x-y)(1+a+xy)=b-c$$ squaring,

$$(1+2xy)((1+a)^2+x^2y^2-2(a+1)xy)=(b+c)^2$$ $$(1-2xy)((1+a)^2+x^2y^2+2(a+1)xy)=(b-c)^2$$

And adding,

$$2(1+a)^2+2x^2y^2-8(a+1)x^2y^2=2(b^2+c^2)$$

So

$$(8a+6)x^2y^2=2(1+a)^2-2(b^2+c^2)$$ $$(4a+3)x^2y^2=(1+a)^2-(b^2+c^2)$$

$$x^2y^2=\frac{(1+a)^2-(b^2+c^2)}{4a+3}$$

On the other hand if we multiply the two equations together we get

$$xy(x^2y^2 +a(1+a))=bc$$

and squaring,

$$x^2y^2(x^2y^2 +a(1+a))^2=b^2c^2$$

and substituting,

$$\frac{(1+a)^2-(b^2+c^2)}{4a+3}\left(\frac{(1+a)^2-(b^2+c^2)} {4a+3} +a(1+a)\right)^2=b^2c^2$$

which becomes,

$$[(1+a)^2-(b^2+c^2)]\left((1+a)(2a+1)^2-(b^2+c^2)\right)^2=b^2c^2(4a+3)^3$$

Answer 4

Hint

...one way of doing this would be firstly to subtract the equations and factorise out $(C-S)$ to get $$(C-S)(1+a+CS)=b-c,$$ where $C=\cos\theta$ and $S=\sin\theta$.

Similarly, you could add the two equations and get $$(C+S)(1+a-CS)=b+c$$

Now square both these equations and add them, writing $x=CS$, and, in doing so you will eliminate the $x^3$ term and get an expression for $x^2$ in terms of $a, b$ and $c$, namely, $$x^2=\frac{(1+a)^2-(b^2+c^2)}{3+4a}$$

Call this $\lambda$, for the moment.

You an then extract $C$ or $S$ by solving a quadratic in either, so, for example $$S^2=\frac{1\pm\sqrt{1-4\lambda}}{2}$$

Now substitute this into the original equation to get the equation satisfied by $a,b$ and $c$.