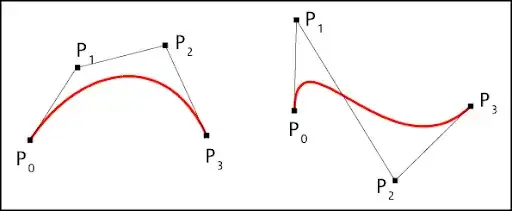
By defining a set of control points $P_i$ a smooth Bézier curve can be constructed. Imagine we have two sets of control points $A={P_i}$ and $B={Q_i}$ that each define a different curve, can we determine if these points collide just based on the sets $A$ and $B$? Or do we have to compute the actual curve?
No.
If the convex hulls of the two curves’ control points do not intersect, then you can conclude that the curves themselves do not intersect (because each curve is contained within the convex hull of its control points).
But if the convex hulls do intersect, you can not make any conclusion about the intersection of the curves — maybe they intersect, or maybe they don’t. You have to do some more serious calculations to decide.
It’s easy to move around the two curves in your picture so that the convex hulls intersect but the curves don’t.
Thank you for spelling Pierre Bézier’s name correctly. Nice to see.
