4

I have this series, and I would like to know if it converges and, if so, for what value.

$$\frac{1}{2}\prod_{n=1}^\infty\frac{\operatorname{prime}(n)-1}{\operatorname{prime}(n)}$$

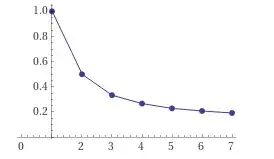
Looking at the plot, it seems to converge:

WolframAlpha result

Trend of the series, from Wolframalpha

Also, considering the values for big n goes close to 1, the series value would converge. What makes sense, considering the small difference that removing 1 should do proportionally in a big number.

$$\frac{\operatorname{prime}(4100000000)-1}{\operatorname{prime}(4100000000)} \approxeq 1 $$

I try to calculate by hand using this recursive function:

$$f(0) = \frac{1}{2}; \qquad f(n) = f(n-1) \cdot \frac{\operatorname{prime}(n)-1}{\operatorname{prime}(n)} $$

I am getting a stable partial result: $f(50000000) \approxeq 0.02711 4$

A similar series, $\frac{1}{2}\prod_{n=2}^\infty\frac{n!-1}{n!} \approxeq 0.1976695 $.

davidlowryduda
  • 91,687
Thiago Mata
  • 143
  • This sequence is decreasing and bounded below by $0$ so yes it converges – Mike Daas Aug 20 '21 at 01:08
  • 2
    The limit is zero, since the prime harmonic series diverges to $+\infty$. – Sangchul Lee Aug 20 '21 at 01:09
  • 1
    We generally prefer to write write $\frac{a_n-1}{a_n}=1-\frac1{a_n}.$ – Thomas Andrews Aug 20 '21 at 01:26
  • 1
    @MikeDaas No, it diverges to zero. – bof Aug 20 '21 at 04:04
  • @bof ''diverges to zero''? That makes no sense. If a sequence has a finite limit, it is said to converge – Mike Daas Aug 20 '21 at 11:02
  • Have a look at the Mertens' theorems. – rtybase Aug 20 '21 at 14:50
  • @MikeDaas Quoting Titchmarsh, The Theory of Functions, 2nd ed., pp. 11–12: "Writing $p_n$ for the partial product $$p_n=\prod_{m=1}^n(1+a_m)$$ we say that the infinite product is convergent if, as $n\to\infty$, the partial product tends to a limit other than zero. We might, of course, admit the limit zero as well, but we shall see later that this would often be inconvenient. If the product is not convergent, it is said to be divergent. If $p_n\to0$, it is said to diverge to zero." – bof Aug 20 '21 at 15:51
  • @MikeDaas Oops, I just noticed that, while the OP asked about convergence of the infinite product (which diverges to zero), your comment mentions the sequence of partial products. You're right of course, the sequence converges to zero. My bad. Sorry about that. – bof Aug 20 '21 at 15:58
  • @bof Ah, I see, thanks for explaining. I suspected this was just a matter of terminology. I was not familiar with that definition of "convergence / divergence" for infinite products. It does not seem very intuitive and in fact mostly confusing to use the same words but with slightly different meanings for products and sequences, as infinite products are simply defined by taking the limit of a sequence. I guess the idea behind it comes from taking the logarithm of the product and considering the convergence or divergence of a sum instead? Also ''diverging to zero'' still sounds odd to me :P – Mike Daas Aug 21 '21 at 00:03

1 Answers1

7

This is the same as $$ \prod_n \Big( 1 - \frac{1}{p_n} \Big),$$ where $p_n$ is the $n$th prime. This would typically be written as $$ \prod_p \Big(1 - \frac{1}{p} \Big).$$ This actually has a name! If you recall the Riemann zeta function, we have $$ \zeta(s) = \sum_{n \geq 1} \frac{1}{n^s} = \prod_p \Big( 1 - \frac{1}{p^s} \Big)^{-1},$$ and so your product is $1/\zeta(1) = 0$.

More generally, the convergence of infinite products is closely related to the convergence of infinite sums. See Proving a result in infinite products: $\prod (1+a_n)$ converges (to a non zero element) iff the series $\sum a_n$ converges. Since it is known that $$ \sum_{p \leq X} \frac{1}{p} \approx \log \log X, $$ the infinite sum diverges very very slowly to $\infty$, and so the product goes to $0$ very very slowly also. (See also Why do we say some infinite products "diverge" when the limit is zero, a finite value? for a confusing terminology).

davidlowryduda
  • 91,687