0

I've made this similar question whose answer doesn't apply to this one.

Given the foci, $F_1$ and $F_2$, and the vertices, $V_1$ and $V_2$, of an hyperbola $\mathcal H$. How can one construct with straight edge and compass the intersections, $A$ and $B$, of $\mathcal H$ and a random secant line $\ell$?

I've tried to figure out one projective transformation of the hyperbola into a circle but I've failed to see it (but on the case in which the hyperbola is rectangular which is the only case I've solved this problem).

hellofriends
  • 1,498

2 Answers2

1

As Intelligenti Pauca pointed out it's possible to do it from the rectangular hyperbola. The drawing gets messy for the whole solution, so it will represent only the dilation part:

enter image description here

EDIT: one does not need to construct $f_1$ neither $f_2$.

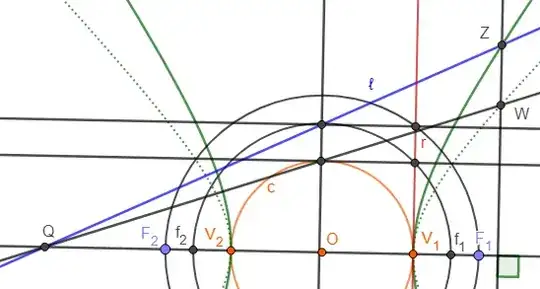
Draw points $f_1$ and $f_2$: the foci of the rectangular hyperbola whose vertices are the same of $\mathcal H$ aka $V_1$ and $V_2$. To do so, take the midpoint $O$ of $F_1$ and $F_2$ and draw a square with side $OV_1$ and construct a circle centered at $O$ and with radius equals to the diagonal of that square. This circle meets line $F_1F_2$ in $f_1$ and $f_2$.

Let $Q = \ell \cap F_1F_2$ and construct the line $\ell '$ which is the image of $\ell$ under the dilation in the $y$ (vertical) axis of ratio $\frac ab$ (parameters of $\mathcal H$). Let $W$ be one of the meetings of $\ell '$ with the rectangular hyperbola of foci $f_1$ and $f_2$ and vertices $V_1$ and $V_2$, then our solution is simply point $Z$: the meeting of the perpendicular to $F_1F_2$ through $W$ with $\ell$.

To solve the rectangular case all we need is to know about this transformation of circles in rectangular hyperbolas:

Given line $s$ and rectangular hyperbola $\mathcal R$ of vertices $V_1$ and $V_2$ we can construct the meetings of $s$ and $\mathcal R$ by drawing the circle $c$, of diameter $V_1V_2$, and the line $r$, tangent to $c$ in $V_1$. Take a random point $P$ in $s$, let $T = PV_2 \cap r$ and let $P'$ be such that $(V_2,T;P,P')=-1$. Let $H = r \cap s$ and $t = \overleftrightarrow{HP'}$, then $\{X_1,X_2\} = t \cap c$ and so the points $x_1 = V_2X_1 \cap s$ and $x_2 = V_2X_2 \cap s$ are the meetings of $s$ and $\mathcal R$

hellofriends
  • 1,498
-1

This problem, I found can be solved (both for an ellipse and a hyperbola) using the elegant construction method as outlined in an answer given to the question:

"Given a point, a line and a circle; how can I find a point on the line having the following property?"

Question asked in math.stackexchange.

To solve the problem for a hyperbola or an ellipse using that construction, you need to make the diameter of the given circle to be equal to the transverse axis/major axis (i.e. equal to the distance between the vertices) with center at one of the foci. The other focus then serves as the given point. There will of course be restrictions on where the given line should go for it to be able to intersect the the conic (in one (tangent) or two points).

I would modify the answer on points 7 and 8 given to the question linked above in the following manner:

  1. Denote by $T_1$ and $T_2$ the points of tangency from point 5 and circle $K$.

  2. Join the center $C$ with $T_1$ and $T_2$ and extend each line ($C$$T_1$, $C$$T_2$) to intersect the given line at points $P_1$ and $P_2$.

The points $P_1$ and $P_2$ are the points on the conic sought for.

For the case of the ellipse the circle will enclose both foci.

Essentially the construction is the solution to the Apollonius problem PPC: See for instance: Cut the knot.

Arne Erikson
  • 81