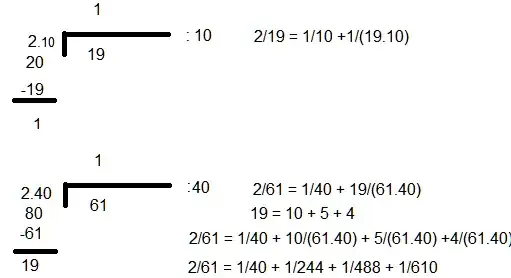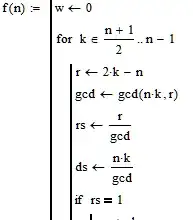0

How the Egyptian fractions (2/n) collected by the scribe Ahmes that are contained in the Rhind papyrus were obtained? The work to obtain them must have been as hard as carrying stones to build a pyramid. For the same fraction, sometimes, we have several options to choose the most convenient according to a certain criterion. I obtained the Egyptian fractions by following two methods. I wanted to measure the work done using a number that is a function of the necessary attempts to obtain the desired result, which consists of two basic steps: obtaining a k factor and looking for the divisors of a certain number. I have a Mathcad program to express 2/n in two, three, and four unit fractions. I needed something more general involving all fractions of denominators 5 to 99. In some attempts to obtain a broader program I got lost in the various “loopings” due to the lack of programming experience. Method #1 starts from the long division method(*). Let the fraction 2/n. Multiply (and then divide) the numerator by a factor k so that the quotient 2.k/n is 1. k belonging to the interval [(n+1)/2;n-1] leaves remainder {1,3,5 ...n-1}. Thus: (2.k/n)/k = 1/k + r/(n.k). Simplify the fraction r/(n.k) by decomposing it into two or three fractions, the new numerators being the divisors (exclusively?) of k. For example: 2/13 [7, 9], [8, 52, 104], [10, 26, 65], [12, 26, 52, 78], [12, 26, 39, 156] work(13) = (12 – 7) + number of possible combinations with divisors (?)

2/19 - 10 < k < 18 (choosing k = 12) (2.12)/19 = 1/12 + 5/(19.12) = 1/12 + 3/(19.12) + 2/(19.12) = 1/12 + 1/76 + 1/114 (Rhind) (5 = 3 + 2) D12={1, 2, 3, 4, 6, 12}

2/35 - 18 < k < 34 (choosing k = 30) (2.30) / 35 = 1/30 + 25 / (35.30) => simplifying => 1/30 + 1 / (7.6) = = 1/30 + 1/42 (Rhind)

2/61 - 31 < k < 60 (choosing k = 40) 2/61 = 1/40 + 19/(61.40) = = 1/40 + 10/(61.40) + 5/(61.40) + 4/(61.40) = = 1/40 + 1/244 + 1/488 + 1/610 (Rhind) (19 = 10 + 5 + 4) D40 = {1, 2, 4, 5, 8, 10, 20, 40}

Method #2 For 2/n = 1/a +1/b + 1/c Multiply 2/n by m.k to get an integer. Decompose this integer into parts so that their sum equals 2.m (i + j + k = 2m). 1 / a = i / (m.k), 1 / b = j / (m.k), 1 / c = k / (m.k) example: 2/13 (choosing m = 8) (2/13). (8.13) = 16 16 = 13 + 2 + 1 2/13 = 13/(8.13) + 2/(8.13) + 1/(8.13) = =1/8 + 1/52 + 1/104

(*)title used to be better understood.. If the Egyptian master asked me to solve the problem of dividing the 9 loaves among 10 men, I would try this reasoning: If I had double the loaves (9x2=18) and divided by 10 I would give one loaf each and the remaining 8 loaves to be divided by 10 (1+8/10). But since I don't have double, I go back and divide by 2, that is, simplifying: 1/2 + (8/10)/2 = 1/2 + 2/5. The 2/5 is on the Table, therefore: 1/2 + (1/3 + 1/15). But I was reprimanded and punished. Why?

division

program

Wilson Massaro
  • 343

1 Answers1

0

According to Gilling's "Mathematics in the times of the pharoahs", there was use made of 'red numbers' or numerators over a common divisor.

To give an idea, consider 2/77. Now, we note that 77 = 7 * 11, and 7 + 11 = 18. By making the numerator 18, we find this is 18/693, = 11/693 + 7/693 = 1/63+1/99.

For the value of 9/10, there are no factors of 10 that make 9. So we could try 18/20, with the same result, or 27/30. This third one is 15/30 + 10/30 + 2/30. We could look at 54/60, which is 30 + 15 + 9 or 15 + 20 + 4.

For large primes, the pattern is to settle on 2 = 1 + 1/2 + 1/3 + 1/6, divided through by p.

Mathematically, the fraction 2/p will need to involve multiples of p, so that the fraction relative to p gives 2. For example, with something like 61, we might look at 63/61 or 124/61.

When we constitute 2x/61x, we seek dividors of 61x that add to 2x. For a fraction 1/x will appear as '61' in the sum, so we can look at composite numbers over 61, where 2x-61 can be comprised of the divisors of x.

70 for example, gives 61+9, which leaves little room

72 gives 61+11 = 61 + 9 + 2. (note 8+3 does not work because 8 deoes not divide 36)

78 gives 61 + 17 = 61 + 13 + 3 + 2 is in with a chance

80 gives 61 + 19 = 61 + 10 + 5 + 4

84 gives 61 + 23 = 61 + 21 + 2

88 gives 61 + 27 = 61 + 22 + 4 + 1

Since there is no means of subtraction, we consider 2/61 as something like 2/61 . x/x. For example, a simple value of x might be 31, gives 62/(6131). Looking somewhat higher, if we consider a number like 72 = 61 + 11, this 11 is 3+8, or 2+9. So we end up with 72/(6136) = 61 + 9 + 2 / (61*36) = 1/36 + 1/122 + 1/546. 84 = 61 + 23 = 61 + 14 + 9, or 96 = 61 + 35, gives 61 + 32 + 3 are possibilities, but these are stretching the point here.

Generally 'red numbers' are the go, not just for 2/x but any fraction. It was commonly used to add several fractions together, by rearranging the sum of numerators over a common denominator.

Note all of these calculations are mental efforts.

wendy.krieger
  • 6,856