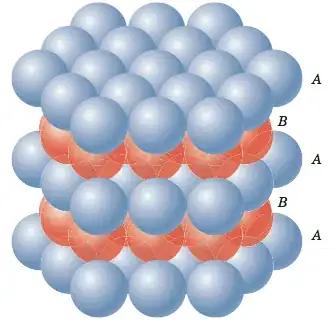
How do I create a HCP using the bottom A layer? In other words, if I take the first layer and make a second layer, how much do I shift it vertically (z direction) and how much do I shift it backwards and forwards (along y axis) each time I make a new layer? In terms of r, the radius of a sphere, would be best.
1 Answers
If we pick any sphere in the bottom layer and an adjacent sphere in the layer above, the displacement vector between their centers tells us how to translate the bottom layer in 3-space to the layer above.
For simplicity, let's pick three adjacent spheres whose centers are nicely situated in the $xy$-plane. Specifically, let one be at the origin $(0,0,0)$, another at $(2,0,0)$, and a third at $(1,\sqrt{3},0)$. (It is well-known that if you cut an equilateral triangle in half, you get a $1$-$\sqrt{3}$-$2$ triangle.)
This triangle sits at the base of a pyramid (regular tetrahedron), the top vertex of which is the center of a sphere in the above layer that is adjacent to the original three.
Exercise. Repeatedly use the Pythagorean theorem to show the centroid of the equilateral triangle must be $(1,\frac{1}{\sqrt{3}},0)$ and the top vertex of the tetrahedron is $(1,\frac{1}{\sqrt{3}},\sqrt{\frac{8}{3}})$.
You can also figure out the angles between various features of this pyramid.
- 151,657