Is there a geometrical reason why for $x\geq 0$ and a natural number $n$, $\frac{x^n-1}{x-1 } = \sum_{i=0}^{n-1} x^i$?

Question

Let $x \geq0$ and $x$ is a real number. And suppose $n$ is a natural number. Thus, $$\frac{x^n-1}{x-1 } = \sum_{i=0}^{n-1} x^i$$ I have proven this with induction but It is some sort of interesting to me that what geometrically reason behind this. While couple days I tried to find a geometrical intuition behind this; but I couldn't find. Now, I suppose it is time to ask for help: First of All, Is there a geometrical thing behind this, and if there is, what is it?

Answer 1

We have $$\forall x \neq 1, \forall n, \sum_{k=0}^{n}x^{k}=\frac{1-x^{n+1}}{1-x}.$$

When $|x|<1$ we can let $n$ tend to infinity to get $\sum_{k=0}^{\infty}x^{k}=\frac{1}{1-x}.$

This is the geometric series. You don't need induction to prove this, just let $S=\sum_{k=0}^{n}x^{k}$ and consider the difference $S-Sx.$

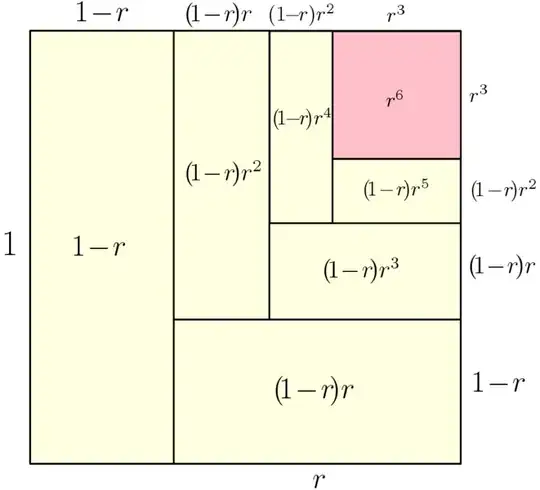
For a geometrical proof of the finite sum of a geometric series consider the following diagram (from here):

The area of the full unit square is equal to the sum of the areas of the yellow rectangles plus the pink square. Thus we have in general:

$$1=(1-r)\sum_{k=0}^{n}r^{k}+r^{n+1},$$

so $$\sum_{k=0}^{n}r^{k}=\frac{1-r^{n+1}}{1-r}$$ as required.

[In this case above we have $n=5.$ For more examples or for the geometrical proof of the infinite sum see here or here]

Answer 2

Even if there is one, it will be difficult to imagine since you need to consider an $n$-dimensional hypercube. (But for integer values of $x$ you might not need to) Here is a possible way (for general real number $x$):

Consider the case $n=3, x>1$. Imagine holding a Rubik's cube by the corner. That corner is $1^3$.

If you slice off that face of the Rubik's cube, you would obtain a square. The rest of the cube has volume $x^2 (x-1)$.

Now consider that face with your corner. If you slice off a row, you would obtain a "line". The rest of the cube has volume $x (x-1)$.

The "line", not including your corner, has volume $(x-1)$.

Thus $x^3 - 1 = (x^2 + x + 1)(x-1)$.

For higher dimension, we can continue this process, slicing off hypercubes. Each time you slice something off, "the number of dimensions" is reduced by 1. But it is very hard to visualize.