For a real $x \in [0, 1)$, does anyone know a non-trivial upper bound for $ \prod_{k = 1}^{n}\left( 1 - x^{k+1}\right) $? Like the fellow here, I am sure I've something like this somewhere... Notice that in my case an upper bound suffices.
-
3You say 'non-trivial' but then you say any upper bound suffices? What about $1$? – QC_QAOA Sep 04 '20 at 18:18
-
Can $x$ take on any real value? Any complex value? Only the values $<1$? Can any of the factors $(1 - x^{k+1})$ be negative? – avs Sep 04 '20 at 18:26
-
2$(1-x^2)$ is also an upper bound. So what do you consider “non-trivial”? – Martin R Sep 04 '20 at 18:28
-
1If the factors $\left(1 - x^{k+1}\right)$ are all positive, then you have $$ \ln \left( \prod_{k=1}^{n} \left(1 - x^{k+1}\right) \right) = \sum_{k=1}^{n} \ln \left(1 - x^{k+1}\right) \leq n \max \left{\ln \left(1 - x^{k+1}\right) ; : ; k = 1, \ldots, n\right}. $$ Is that something you were looking for? – avs Sep 04 '20 at 18:29
-
1A more sophisticated bound might be obtained by comparing $$ \sum_{k=1}^{n} \ln \left(1 - x^{k+1}\right) $$ to an appropriate integral, something like $$ \int_{s=0}^{n} \ln \left(1 - x^{s+1}\right) ds. $$ – avs Sep 04 '20 at 18:31
-
Hi @QC_QAOA! By non-trivial I meant 1, indeed. – JFarias Sep 04 '20 at 19:39
-
Hi @avs! Any real value in $[0, 1)$, therefore $1 - x^{k+1} > 0$, $\forall k$. – JFarias Sep 04 '20 at 19:41
-
Hi @MartinR, oh sure, $(1 - x^2)$ would work for me actually, but I was thought there was an expression, like a definite integral. I guess that was already pointed that out. – JFarias Sep 04 '20 at 19:46
-
1@avs, cool! I'll check if that integral works for me. I was indeed just looking for a bound that was not "1". Thanks for you help! – JFarias Sep 04 '20 at 19:48
1 Answers
Write $f(x)$ for your function. I'll be detailed here since this is a nice pedagogical example. Since all the terms are positive an equivalent problem is to upper bound the logarithm
$$\log f(x) = \sum_{k=1}^n \log (1 - x^{k+1}).$$
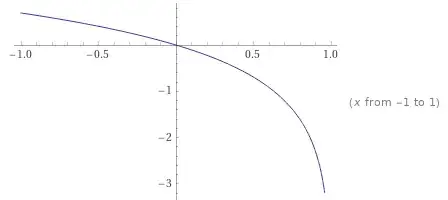
Any upper bound on the function $\log (1 - r)$ on the interval $r \in [0, 1)$ then provides a bound on this sum. Let's remind ourselves what $\log (1 - r)$ looks like; here is a plot from WolframAlpha:
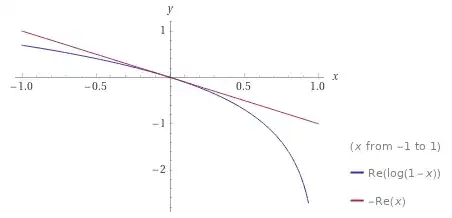
In particular it's decreasing and concave. $0$ is a trivial upper bound, which gives the trivial upper bound $1$ on the product as mentioned in the comments. A more interesting upper bound is the linear Taylor approximation at the origin, which is $1 - r$. Here's a plot of the two of them together:
This gives us the famous inequality $\log (1 - r) \le -r$, which may be more familiar in exponential form $1 - r \le e^{-r}$. Applying this inequality to each term of the sum above gives a sum of geometric series
$$\log f(x) \le \sum_{k=1}^n -x^{k+1} = -x^2 \left( \frac{1 - x^n}{1 - x} \right)$$
and exponentiating gives
$$\boxed{ f(x) \le \exp \left( -x^2 \left( \frac{1 - x^n}{1 - x} \right) \right) }.$$
This bound is designed to be particularly good for small $x$; it becomes less and less accurate for larger $x$ since the same is true of the Taylor approximation we used, and note that at $x = 1$ it gives $f(1) \le \exp (-n)$ whereas in fact $\lim_{x \nearrow 1} f(x) = 0$.
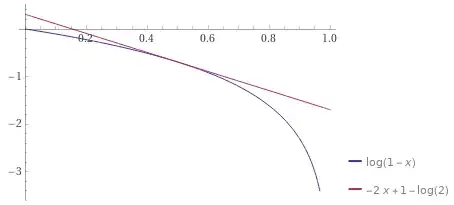
Fortunately, since $\ln (1 - r)$ is concave it lies below all of its tangent lines, so depending on what values of $x$ you're interested in you can replace the bound we used above by other linear bounds. For example, the linear Taylor approximation at $r = \frac{1}{2}$ gives
$$\ln (1 - r) \le -2r - \ln 2 + 1.$$
Here's what this one looks like:
Of course, as other commenters have said, it's hard to know what kind of bounding is appropriate here if we don't know what you're planning on using them for; for some purposes the bound $f(x) \le 1$ might suffice.
- 419,620