0

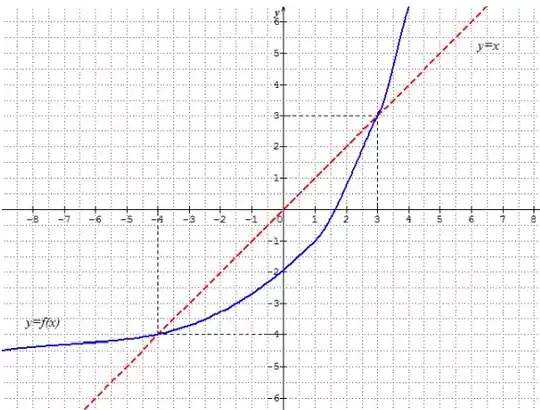
Let $A_n$ be a sequence such that $A_0\in\mathbb R$ and $A_{n+1}=f(A_n)$. Is it possible to choose value for $A_0$ such that $A_n$ is a monotonic geometric sequence or a monotonic arithmetic sequence?

My attempt:

I started from the 3 regions:

1- If $A_n$ is an arithmetic sequence, then $A_{n+1}=A_n + d\implies f(x)=x+d\implies f-x=cst$, which is not true $\forall x$.

2- If $A_n$ is a geometric sequence, then we have $A_{n+1} =A_n \cdot d\implies f=xd$ which is also not true $\forall x$.

My conclusion is that we can't find a value for $A_0$ such that $A_n$ is either a geometric or an arithmetic sequence.

Is my answer wrong?

enter image description here

Alessio K
  • 10,599
Hasan
  • 57
  • does a0 determine whether the sequence is increasing or decreasing ? , is there a general method to find if An+1 is geometric or arithmetic ? – Hasan Sep 02 '20 at 17:25
  • 1
    What is $f$? Is it given to you or can you pick it? – Qiaochu Yuan Sep 02 '20 at 17:29
  • it's the blue curve – Hasan Sep 02 '20 at 17:31
  • @Hasan your approach is not correct because it is a recurrent sequence. Did you have an explanation where the line $y=x$ is a mirror which helps to draw the terms of the sequence in the given figure? – user376343 Sep 02 '20 at 18:08
  • 1
    If $a_0=-4$ or $a_0=3,$ the sequence is constant. Therefore it is both arithmetic and geometric. If $a_0\in (-\infty,3),$ the sequence is attracted to $-4.$ Therefore it cannot be arithmetic, but theoretically could be geometric (it is to verify). If $a_0\in (3,\infty),$ the sequence diverges to infinity. Now, it could be arithmetic or geometric, but this has to be verified – user376343 Sep 02 '20 at 18:09
  • @user376343 if a0 belong to - infinity to 3 or 3 to infinity the sequence will not be geometric i tried using two values for each , similarly it's not arithmetic for a0 > 3 – Hasan Sep 02 '20 at 18:31
  • @user376343 No, the given is the graph only – Hasan Sep 02 '20 at 18:32
  • @Hasan do you understand French? If yes, this web can be helpful. See video in section "Construction graphique" https://www.methodemaths.fr/suites/ – user376343 Sep 02 '20 at 18:42
  • Let us continue this discussion in chat. – Hasan Sep 02 '20 at 20:28
  • You appear to have not understood the question. Your arguments in both the post and comments deduce impossibility because of certain examples only. But the problem does NOT ask if every such sequence $A_n$ is arithmetic or geometric. It asks if there are any values of $A_0$ that could be chosen to make it one or the other. I.e., to show it is true you need only one example of each. To show it false, you have to prove that every sequence is not arithmetic or geometric. user376343 has already supplied you with the answer above. – Paul Sinclair Sep 03 '20 at 03:47
  • @PaulSinclair i did'nt understand " if every such sequence An" , does An count as one sequence ? – Hasan Sep 03 '20 at 11:51
  • 1
    Each possible choice for $A_0$ determines a different sequence. It may help to think of "${A_n}$" not as "a" sequence, but as a map that carries $x \in \Bbb R$ to the sequence $x, f(x), f(f(x)), f(f(f(x)))), ...$. The question is, "are there any values of $x$ that will cause the resulting sequence to be either arithmetic or geometric". But your arguments address "does every value of $x$ result in an arithmetic or geometric sequence", which is a different question. – Paul Sinclair Sep 03 '20 at 13:41
  • clear thank you – Hasan Sep 03 '20 at 14:31

0 Answers0